��Ŀ����
��2013•������һģ����ƽ��ֱ������ϵxOy�У�������y=x2-2mx+m2-9��x�ύ��A��B���㣨��A�ڵ�B����࣬��OA��OB������y��Ľ�������Ϊ��0��-5������M���߶�AB�ϵ�����һ�㣬����M��a��0����ֱ��MC��x�ᣬ���������ڵ�C���ǵ�C���������߶Գ���ĶԳƵ�ΪD��C��D���غϣ�����P���߶�MC��һ�㣬����CD��BD��PD��
��1����������ߵĽ���ʽ��
��2����a=1ʱ���ʵ�P��ʲôλ��ʱ����ʹ��PD��BD��
��3������P����MP=
MC����PE��PD��x���ڵ�E�����Ƿ���������ĵ�E��ʹ��PE=PD�������ڣ������E�����ꣻ�������ڣ���˵�����ɣ�
��1����������ߵĽ���ʽ��
��2����a=1ʱ���ʵ�P��ʲôλ��ʱ����ʹ��PD��BD��
��3������P����MP=
| 1 | 4 |

��������1��ֱ�ӽ�C�㣨0��-5������y=x2-2mx+m2-9������������x�ύ��A��B���㣨��A�ڵ�B����࣬��OA��OB�������m��ֵ���ɣ�
��2����D����DF��x���ڵ�F������ֱ�������ε����ʿ��Եó���PDC=��BDF���Ӷ����������PCD�ס�BFD�������������ε����ʾͿ���������ۣ�
��3������E�������ֱ�������ε����ʿ��Եó���MEP=��CPD���ٸ����������Եó���EPM�ա�PDC����PM=DC��EM=PC����C��x0��y0������D��4-x0��y0����P(x0��
y0)������PM=DC����|2x0-4|=-
y0����C��������������|2x0-4|=-
(
-4x0-5)��������������x0��ֵ�Ϳ��Եó����ۣ�
��2����D����DF��x���ڵ�F������ֱ�������ε����ʿ��Եó���PDC=��BDF���Ӷ����������PCD�ס�BFD�������������ε����ʾͿ���������ۣ�
��3������E�������ֱ�������ε����ʿ��Եó���MEP=��CPD���ٸ����������Եó���EPM�ա�PDC����PM=DC��EM=PC����C��x0��y0������D��4-x0��y0����P(x0��
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| x | 2 0 |
����⣺��1����������y=x2-2mx+m2-9��y�ύ������Ϊ��0��-5����
��-5=m2-9��
��ã�m=��2��
��m=-2��y=0ʱ��x2+4x-5=0
��ã�x1=-5��x2=1��
��������y=x2-2mx+m2-9��x�ύ��A��B���㣨��A�ڵ�B����࣬��OA��OB����
��m=-2���������⣬��ȥ��
��m=2��
�������ߵĽ���ʽΪy=x2-4x-5��
��2����D����DF��x���ڵ�F��
���DFB=90��
��MC��x�ᣬ
���CMB=90�㣬
���CMB=��DFB��
��CM��DF��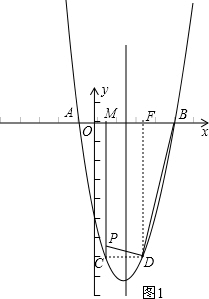
��C��D���������ߵĶԳ���Գƣ�
��CD��x�ᣬ
���MCD=��CDF=��CDP+��PDF=90��
��PD��BD��
���PDB=��PDF+��FDB=90��
���PDC=��BDF��
�ߡ�PCD=��BFD=90�㣬
���PCD�ס�BFD��
��
=
��
��x=1ʱ��y=-8��
��C��1��-8����D��3��-8����F��3��0����B��5��0����
��P��1��y����
��
=
��
��ã�y=-
��
�൱P������Ϊ(1��-
)ʱ��PD��BD��
��3������E����ڣ���MC��EM��CD��MC��
���EMP=��PCD=90�㣮
���MEP+��MPE=90��
��PE��PD��
���EPD=90�㣬
���MPE+��DPC=90��
���MEP=��CPD��
�ڡ�EMP�͡�PCD�У�
��
���EPM�ա�PDC��AAS����
��PM=DC��EM=PC��
��C��x0��y0������D��4-x0��y0����P(x0��
y0)��
��|2x0-4|=-
y0��
�ߵ�C��������y=x2-4x-5�ϣ�
��y0�Tx02-4x0-5
��|2x0-4|=-
(
-4x0-5)��
��2x0-4=-
(
-4x0-5)ʱ��
��ã�x01=3��x02=-7����ȥ����
��4-2x0=-
(
-4x0-5)ʱ��
��ã�x03=1��x04=11����ȥ����
��x0=1��x0=3��
��P��1��-2����P��3��-2����
��PC=6����ME=PC=6��
��E��7��0����E��-3��0����
��-5=m2-9��
��ã�m=��2��
��m=-2��y=0ʱ��x2+4x-5=0
��ã�x1=-5��x2=1��
��������y=x2-2mx+m2-9��x�ύ��A��B���㣨��A�ڵ�B����࣬��OA��OB����
��m=-2���������⣬��ȥ��
��m=2��
�������ߵĽ���ʽΪy=x2-4x-5��
��2����D����DF��x���ڵ�F��
���DFB=90��
��MC��x�ᣬ
���CMB=90�㣬
���CMB=��DFB��
��CM��DF��

��C��D���������ߵĶԳ���Գƣ�
��CD��x�ᣬ
���MCD=��CDF=��CDP+��PDF=90��
��PD��BD��
���PDB=��PDF+��FDB=90��
���PDC=��BDF��
�ߡ�PCD=��BFD=90�㣬
���PCD�ס�BFD��
��
| CD |
| FD |
| PC |
| BF |
��x=1ʱ��y=-8��
��C��1��-8����D��3��-8����F��3��0����B��5��0����
��P��1��y����
��
| 2 |
| 8 |
| y+8 |
| 2 |
��ã�y=-
| 15 |
| 2 |
�൱P������Ϊ(1��-
| 15 |
| 2 |
��3������E����ڣ���MC��EM��CD��MC��
���EMP=��PCD=90�㣮
���MEP+��MPE=90��
��PE��PD��
���EPD=90�㣬
���MPE+��DPC=90��
���MEP=��CPD��
�ڡ�EMP�͡�PCD�У�
|
���EPM�ա�PDC��AAS����
��PM=DC��EM=PC��

��C��x0��y0������D��4-x0��y0����P(x0��
| 1 |
| 4 |
��|2x0-4|=-
| 1 |
| 4 |
�ߵ�C��������y=x2-4x-5�ϣ�
��y0�Tx02-4x0-5
��|2x0-4|=-
| 1 |
| 4 |
| x | 2 0 |
��2x0-4=-
| 1 |
| 4 |
| x | 2 0 |
��ã�x01=3��x02=-7����ȥ����
��4-2x0=-
| 1 |
| 4 |
| x | 2 0 |
��ã�x03=1��x04=11����ȥ����
��x0=1��x0=3��
��P��1��-2����P��3��-2����
��PC=6����ME=PC=6��
��E��7��0����E��-3��0����
������������һ�����κ������ۺ����⣬���������ô���ϵ������һ�κ����Ľ���ʽ�����ã����������ε��ж������ʵ����ã�ȫ�������ε��ж������ʵ����ã�ֱ�������ε����ʵ����ã����ʱ�����ô���ϵ�����������ʽ�ǹؼ���������������ֱ�������ε��������ص��ѵ㣮

��ϰ��ϵ�д�
�����Ŀ
 ��2013•������һģ����֪ÿ��������С�����εı߳�����1����ͼ�е���Ӱͼ�����������Ը��ΪԲ�ģ��뾶�ֱ�Ϊ1��2��Բ��Χ�ɣ�����Ӱ���ֵ������
��2013•������һģ����֪ÿ��������С�����εı߳�����1����ͼ�е���Ӱͼ�����������Ը��ΪԲ�ģ��뾶�ֱ�Ϊ1��2��Բ��Χ�ɣ�����Ӱ���ֵ������ ��2013•������һģ����ƽ��ֱ������ϵ�У�������ABCD��λ����ͼ��ʾ����A������Ϊ��1��0������D������Ϊ��0��2�����ӳ�CB��x���ڵ�A1����������A1B1C1C���ӳ�C1B1��x���ڵ�A2����������A2B2C2C1�����������Ĺ��ɽ�����ȥ����2013�������ε����Ϊ
��2013•������һģ����ƽ��ֱ������ϵ�У�������ABCD��λ����ͼ��ʾ����A������Ϊ��1��0������D������Ϊ��0��2�����ӳ�CB��x���ڵ�A1����������A1B1C1C���ӳ�C1B1��x���ڵ�A2����������A2B2C2C1�����������Ĺ��ɽ�����ȥ����2013�������ε����Ϊ