摘要:如图:等边三角形ABC的边长为1 ,P为AB边上的一个动点,过P作PQ⊥BC于Q,过Q作QR⊥AC于R,再过R作RS⊥AB于S .设AP=x,AS=y. (1) 求y与x之间的函数关系式,并写出自变量取值范围. (2) 若SP=1/4,求AP的长. (3) A R Q C B S P 若S.P重合点为T.试说明当P.S不重合时,P.S中的哪一个更接近T点?将上述操作.即按逆时针方向.过垂足作相邻边的垂线.若操作不断进行.试依据你的结论.猜想无论P的初始位置如何.P.S--等这些点最终将会出现怎样的趋势?
网址:http://m.1010jiajiao.com/timu3_id_437441[举报]
等边三角形
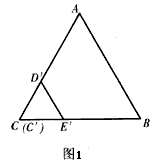
ABC的边长为3 cm,边长为1 cm的等边三角形RPQ的顶点R与点A重合,P、Q两点分别在AC、AB上.将△RPQ沿着边AB、BC、CA顺时针连续翻转(如图所示),直至点P第一次回到原来的位置,则点P运动的路径长为________cm.
等边三角形ABC的边AB在直线l上,动点D也在直线l上(不与A,B点重合),△ADE为等边三角形.
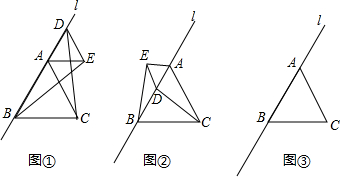
(1)如图①,当点D在线段BA的延长线上且△ADE与△ABC在直线l的同侧时,试猜想线段BE与CD的大小关系为
(2)如图②,当点D在线段BA上且ADE与ABC在直线l异测时,(1)中的结论是否仍然成立?若不成立,请说明结论发生了怎样的变化;若成立,说明理由,并求出此时线段BE与CD所在直线的夹角α(0°<α<90°)
(3)当点D在线段AB的延长线上且△ADE与△ABC仍然在直线l的异测时,试在图中画③出相应的图形,并直接判断此时BE与CD的关系(不必说明理由).

查看习题详情和答案>>
(1)如图①,当点D在线段BA的延长线上且△ADE与△ABC在直线l的同侧时,试猜想线段BE与CD的大小关系为
BE=CD
BE=CD
(2)如图②,当点D在线段BA上且ADE与ABC在直线l异测时,(1)中的结论是否仍然成立?若不成立,请说明结论发生了怎样的变化;若成立,说明理由,并求出此时线段BE与CD所在直线的夹角α(0°<α<90°)
(3)当点D在线段AB的延长线上且△ADE与△ABC仍然在直线l的异测时,试在图中画③出相应的图形,并直接判断此时BE与CD的关系(不必说明理由).


 和2。
和2。