题目内容
等边三角形纸片ABC和C'D'E'的边长分别为 和2。
和2。
 和2。
和2。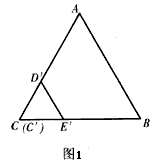


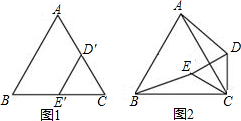
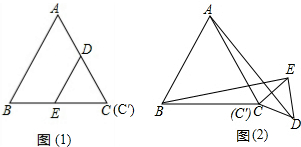
(1)如图1,将△C'D'E'放在△ABC上,使得C'和C重合,且D'和E'分别AC在AC和BC上,固定△ABC,将△C'D'E'绕点C逆时针旋转30°得到△C'DE(如图2),连接AD、BE,C'E的延长线交AB于F,试判断线段BE与AD的数量关系,并证明你的结论;
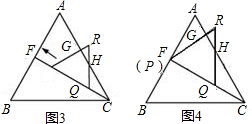
(2)如图,若将△C'DE继续移动,使其在线段CF上沿着CF的方向以每秒1个单位的速度平移,如图3,设△C'DE移动的时间为x秒,△C'DE与△ABC重叠部分的面积为y,求y与x之间的函数关系式,并求出自变量x的取值范围。
(2)如图,若将△C'DE继续移动,使其在线段CF上沿着CF的方向以每秒1个单位的速度平移,如图3,设△C'DE移动的时间为x秒,△C'DE与△ABC重叠部分的面积为y,求y与x之间的函数关系式,并求出自变量x的取值范围。
解:(1)BE与AD的关系是相等,
证明:∵△ABC与△C'D'E'是等边三角形,
∴DC=EC,AC=BC,∠ABC=∠DCE
∵∠ACF=∠ACF
∴∠DCA=∠ECB
∴在△ADC和△ECB中,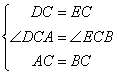
∴△ADC≌△ECB
∴BE=AD。
(2)∵∠BCF=30°
∴ ∠BCF=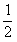 ∠ACB=∠ACF
∠ACB=∠ACF
∴CF⊥AB于F
∵BC=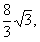
∴在Rt△BFC中,BF=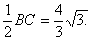
由勾股定理得CF=4,
∵C'E=2,且△C'DE平移的速度是1
∴0≤x≤2
∵∠DC'E=60°,∠ACF=30°,
∴∠CGC'=30°
∴∠ACF=∠CGC'
∴DG=2-x
又∵∠D=60°,∠DGH=30°,
∴∠DHG=90°
∴△DGH为直角三角形
∴DH=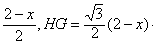
∴S△DGH=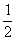 ×DH×HG=
×DH×HG=
又∵S△DC'E=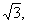
∴ y=S△DC'E-S△DGH=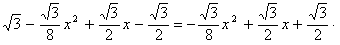
∴ 。
。
证明:∵△ABC与△C'D'E'是等边三角形,
∴DC=EC,AC=BC,∠ABC=∠DCE
∵∠ACF=∠ACF
∴∠DCA=∠ECB
∴在△ADC和△ECB中,
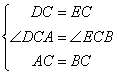
∴△ADC≌△ECB
∴BE=AD。
(2)∵∠BCF=30°
∴ ∠BCF=
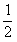 ∠ACB=∠ACF
∠ACB=∠ACF∴CF⊥AB于F
∵BC=
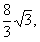
∴在Rt△BFC中,BF=
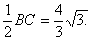
由勾股定理得CF=4,
∵C'E=2,且△C'DE平移的速度是1
∴0≤x≤2
∵∠DC'E=60°,∠ACF=30°,
∴∠CGC'=30°
∴∠ACF=∠CGC'
∴DG=2-x
又∵∠D=60°,∠DGH=30°,
∴∠DHG=90°
∴△DGH为直角三角形
∴DH=
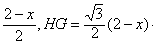
∴S△DGH=
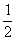 ×DH×HG=
×DH×HG=
又∵S△DC'E=
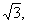
∴ y=S△DC'E-S△DGH=
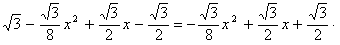
∴
 。
。
练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目

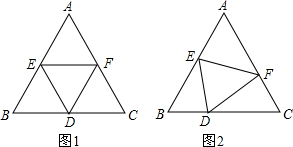
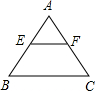 如图,一张边长为4的等边三角形纸片ABC,点E是边AB上的一个动点(不与A、B重合),EF∥BC交AC于点F.以EF为折痕对折纸片,当△AEF与四边形EBCF重叠部分的面积为
如图,一张边长为4的等边三角形纸片ABC,点E是边AB上的一个动点(不与A、B重合),EF∥BC交AC于点F.以EF为折痕对折纸片,当△AEF与四边形EBCF重叠部分的面积为