摘要：铺成一片可以不留空隙的平面图形有 ,
网址：http://m.1010jiajiao.com/timu3_id_436656[举报]
下列各题中解题方法或说法正确的个数有（ ）
（1）用换元法解方程
+
+3=0，设
=y，则原方程可化为y+
+3=0；
（2）若x+y=a，x-y=b，求2x2+2y2的值．用配方法求，2x2+2y2=（x+y）2+（x-y）2；
（3）若x2-4x+4+
=0，求x、y的值．用非负数的和为零解，则原式可以化为（x-2）2+
=0；
（4）四个全等的任意四边形的地砖，铺成一片可以不留空隙．
（1）用换元法解方程
| x |
| x-1 |
| 2x-2 |
| x |
| x |
| x-1 |
| 2 |
| y |
（2）若x+y=a，x-y=b，求2x2+2y2的值．用配方法求，2x2+2y2=（x+y）2+（x-y）2；
（3）若x2-4x+4+
| y-6 |
| y-6 |
=0；
（4）四个全等的任意四边形的地砖，铺成一片可以不留空隙．
| A、1个 | B、2个 | C、3个 | D、4个 |
下列各题中解题方法或说法正确的个数有（ ）
（1）用换元法解方程
+
+3=0，设
=y，则原方程可化为y+
+3=0；
（2）若x+y=a，x-y=b，求2x2+2y2的值．用配方法求，2x2+2y2=（x+y）2+（x-y）2；
（3）若x2-4x+4+
=0，求x、y的值．用非负数的和为零解，则原式可以化为（x-2）2+
=0；
（4）四个全等的任意四边形的地砖，铺成一片可以不留空隙．
查看习题详情和答案>>
（1）用换元法解方程
| x |
| x-1 |
| 2x-2 |
| x |
| x |
| x-1 |
| 2 |
| y |
（2）若x+y=a，x-y=b，求2x2+2y2的值．用配方法求，2x2+2y2=（x+y）2+（x-y）2；
（3）若x2-4x+4+
| y-6 |
| y-6 |
=0；
（4）四个全等的任意四边形的地砖，铺成一片可以不留空隙．
| A．1个 | B．2个 | C．3个 | D．4个 |
（2002•十堰）下列各题中解题方法或说法正确的个数有（ ）
（1）用换元法解方程
+
+3=0，设
=y，则原方程可化为y+
+3=0；
（2）若x+y=a，x-y=b，求2x2+2y2的值．用配方法求，2x2+2y2=（x+y）2+（x-y）2；
（3）若x2-4x+4+
=0，求x、y的值．用非负数的和为零解，则原式可以化为（x-2）2+
=0；
（4）四个全等的任意四边形的地砖，铺成一片可以不留空隙．
A．1个
B．2个
C．3个
D．4个
查看习题详情和答案>>
（1）用换元法解方程
++3=0，设=y，则原方程可化为y++3=0；（2）若x+y=a，x-y=b，求2x2+2y2的值．用配方法求，2x2+2y2=（x+y）2+（x-y）2；
（3）若x2-4x+4+
=0，求x、y的值．用非负数的和为零解，则原式可以化为（x-2）2+=0；
（4）四个全等的任意四边形的地砖，铺成一片可以不留空隙．
A．1个
B．2个
C．3个
D．4个
查看习题详情和答案>>
+
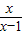+3=0，设
=y，则原方程可化为y+
+3=0；
=0，求x、y的值．用非负数的和为零解，则原式可以化为（x-2）2+
+
+3=0，设
=y，则原方程可化为y+
+3=0；
=0，求x、y的值．用非负数的和为零解，则原式可以化为（x-2）2+