题目内容
下列各题中解题方法或说法正确的个数有( )
(1)用换元法解方程
+
+3=0,设
=y,则原方程可化为y+
+3=0;
(2)若x+y=a,x-y=b,求2x2+2y2的值.用配方法求,2x2+2y2=(x+y)2+(x-y)2;
(3)若x2-4x+4+
=0,求x、y的值.用非负数的和为零解,则原式可以化为(x-2)2+
=0;
(4)四个全等的任意四边形的地砖,铺成一片可以不留空隙.
(1)用换元法解方程
| x |
| x-1 |
| 2x-2 |
| x |
| x |
| x-1 |
| 2 |
| y |
(2)若x+y=a,x-y=b,求2x2+2y2的值.用配方法求,2x2+2y2=(x+y)2+(x-y)2;
(3)若x2-4x+4+
| y-6 |
| y-6 |
=0;
(4)四个全等的任意四边形的地砖,铺成一片可以不留空隙.
| A.1个 | B.2个 | C.3个 | D.4个 |
(1)设
=y,则
=
,原方程可化为y+
+3=0.正确;
(2)运用完全平方公式.正确;
(3)要想让等式成为0,则必须让根号里的和平方都为0,正确;
(4)因为四边形的内角和为360°,铺成一片可以不留空隙,正确.
故选D.
| x |
| x-1 |
| 2x-2 |
| x |
| 2 |
| y |
| 2 |
| y |
(2)运用完全平方公式.正确;
(3)要想让等式成为0,则必须让根号里的和平方都为0,正确;
(4)因为四边形的内角和为360°,铺成一片可以不留空隙,正确.
故选D.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
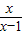 +
+ +3=0,设
+3=0,设 =y,则原方程可化为y+
=y,则原方程可化为y+ +3=0;
+3=0; =0,求x、y的值.用非负数的和为零解,则原式可以化为(x-2)2+
=0,求x、y的值.用非负数的和为零解,则原式可以化为(x-2)2+
 +
+ +3=0,设
+3=0,设 =y,则原方程可化为y+
=y,则原方程可化为y+ +3=0;
+3=0; =0,求x、y的值.用非负数的和为零解,则原式可以化为(x-2)2+
=0,求x、y的值.用非负数的和为零解,则原式可以化为(x-2)2+
 +
+ +3=0,设
+3=0,设 =y,则原方程可化为y+
=y,则原方程可化为y+ +3=0;
+3=0; =0,求x、y的值.用非负数的和为零解,则原式可以化为(x-2)2+
=0,求x、y的值.用非负数的和为零解,则原式可以化为(x-2)2+