摘要： 如图.已知直角坐标系内有一条直线和一条曲线.这条直线和x轴.y轴分别交于点A和点B.且OA＝OB＝1.这条曲线是函数y＝的图像在第一限内的一个分支.点P是这条曲线的任意一点.它的坐标是(a.b).由点P向x轴.y轴所作的垂线PM.PN分别与直线AB相交于点E和F. 1) 求△OEF的面积, 2) △AOF与△BOE是否一定相似.如果一定相似.请证明,如果不一定相似.请说明理由, 3) 当点P在曲线上移动时.△OEF随之变动.指出在△OEF的三个内角中.是否有大小始终保持不变的角?若有.请求出其大小,若没有.请说明理由.
网址：http://m.1010jiajiao.com/timu3_id_436583[举报]
如图，已知直角坐标系内有一条直线和一条曲线，这条直线和x轴、y轴正半轴分别交于点A和点B，且OA=OB=1．这条曲线是函数y=
的图象在第一象限的一个分支，点P是这条曲线上任意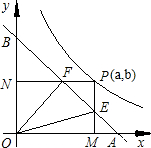
一点，它的坐标是（a、b），由点P向x轴、y轴所作的垂线PM、PN，垂足是M、N，直线AB分别交PM、PN于点E、F．
（1）分别求出点E、F的坐标（用a的代数式表示点E的坐标，用b的代数式表示点F的坐标，只须写出结果，不要求写出计算过程）；
（2）求△OEF的面积（结果用含a、b的代数式表示）；
（3）分别计算AF与BE的值（结果用含a、b的代数式表示）；
（4）△AOF与△BOE是否一定相似，请予以证明；如果不一定相似或一定不相似，简要说明理由． 查看习题详情和答案>>
| 1 | 2x |
一点，它的坐标是（a、b），由点P向x轴、y轴所作的垂线PM、PN，垂足是M、N，直线AB分别交PM、PN于点E、F．（1）分别求出点E、F的坐标（用a的代数式表示点E的坐标，用b的代数式表示点F的坐标，只须写出结果，不要求写出计算过程）；
（2）求△OEF的面积（结果用含a、b的代数式表示）；
（3）分别计算AF与BE的值（结果用含a、b的代数式表示）；
（4）△AOF与△BOE是否一定相似，请予以证明；如果不一定相似或一定不相似，简要说明理由． 查看习题详情和答案>>
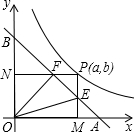如图，已知直角坐标系内有一条直线和一条曲线，这条直线和x轴、y轴分别交于点A和点B，且OA=OB=1．这条曲线是函数y=| 1 | 2x |
如图，已知直角坐标系内有一条直线和一条曲线，这条直线和x轴、y轴分别交于点A和点B，且OA=OB=1，这条曲线是函数y=
的图象在第一限内的一个分支，点P是这条曲线的任意一点，它的坐标是（a，b），由点P向x轴、y轴所作的垂线PM、PN（点M、N为垂足）分别与直线AB相交于点E和F．
（1）求△OEF的面积（a，b的代数式表示）；
（2）△AOF与△BOE是否一定相似？如果一定相似，请证明；如果不一定相似，请说明理由；
（3）当点P在曲线上移动时，△OEF随之变动，指出在△OEF的三个内角中，是否有大小始终保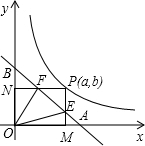
持不变的角？若有，请求出其大小；若没有，请说明理由．
查看习题详情和答案>>
| 1 | 2x |
（1）求△OEF的面积（a，b的代数式表示）；
（2）△AOF与△BOE是否一定相似？如果一定相似，请证明；如果不一定相似，请说明理由；
（3）当点P在曲线上移动时，△OEF随之变动，指出在△OEF的三个内角中，是否有大小始终保
持不变的角？若有，请求出其大小；若没有，请说明理由．
查看习题详情和答案>>
如图，已知直角坐标系内有一条直线和一条曲线，这条直线和x轴、y轴分别交于点A和点B，且OA=OB=1．这条曲线是函数y=
的图象在第一象限的一个分支，点P是这条曲线上任意一点，它的坐标是（a、b），由点P向x轴、y轴作垂线PM、PN，垂足是M、N，直线AB分别交PM、PN于点E、F．
（1）点E坐标是
（2）求△OEF的面积（结果用含a、b的代数式表示）；
（3）△AOF与△BOE是否相似？若相似，请证明；若不相似，请简要说明理由．
（4）当点P在曲线y=
上移动时，△OEF随之变动，指出在△OEF的三个内角中，大小始终保持不变的那个角，并求出此角的大小，同时证明你的结论．
查看习题详情和答案>>
| 1 |
| 2x |
（1）点E坐标是
（a，1-a）
（a，1-a）
，点F坐标是（1-b，b）
（1-b，b）
（用含a的代数式表示点E的坐标，用含b的代数式表示点F的坐标）（2）求△OEF的面积（结果用含a、b的代数式表示）；
（3）△AOF与△BOE是否相似？若相似，请证明；若不相似，请简要说明理由．
（4）当点P在曲线y=
| 1 |
| 2x |
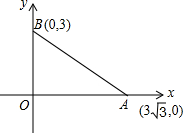如图，已知直角坐标系内两点A