题目内容
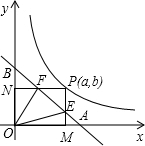
如图,已知直角坐标系内有一条直线和一条曲线,这条直线和x轴、y轴分别交于点A和点B,且OA=OB=1,这条曲线是函数y=| 1 | 2x |
(1)求△OEF的面积(a,b的代数式表示);
(2)△AOF与△BOE是否一定相似?如果一定相似,请证明;如果不一定相似,请说明理由;
(3)当点P在曲线上移动时,△OEF随之变动,指出在△OEF的三个内角中,是否有大小始终保
 持不变的角?若有,请求出其大小;若没有,请说明理由.
持不变的角?若有,请求出其大小;若没有,请说明理由.
分析:(1)欲求△OEF的面积,只要求出E、F坐标即可.根据矩形性质、直线AB解析式容易求出;
(2)根据题意易知∠A=∠B,要证△AOF与△BOE相似,只证夹边对应成比例即可;
(3)应用三角形内角和定理及内外角关系可求∠EOF=45°是一定值,即解.
(2)根据题意易知∠A=∠B,要证△AOF与△BOE相似,只证夹边对应成比例即可;
(3)应用三角形内角和定理及内外角关系可求∠EOF=45°是一定值,即解.
解答:解:(1)根据题意,易知:直线AB的解析式为y=-x+1,
点E的坐标是(a,1-a),点F的坐标是(1-b,b),
当PM、PN与线段AB都相交时,如图1,
∴S△EOF=S△AOB-S△AOE-S△BOF
=
×1×1-
×1×(1-a)-
×1×(1-b)
=
,
当PM、PN中有一条与AB相交,另一条与BA延长线或AB延长线相交时,如图2和图3,
∴S△EOF=S△FOA+S△AOE=
×1×b+
×1×(a-1)=
,
∴S△EOF=S△FOB+S△BOE=
×1×(b-1)+
×1×a=
,
即S△EOF=
;
(2)△AOF和△BEO一定相似.
∵如图1,OA=OB=1,
∴∠OAF=∠EBO,
∴BE=BA-AE=
-
=
a,
AF=BA-BF=
-
=
b,
∵点P是函数y=
图象上任意一点,
∴b=
,即2ab=1,
∴
a×
b=1即,AF•BE=OB•OA,
∴
=
,
∴△AOF∽△BEO,
∵对图2,图3同理可证,
∴△AOF∽△BEO;
(3)当点P在曲线上移动时,在△OEF中,∠EOF一定等于45°,
由(2)知,△AOF∽△BEO,
∴∠AFO=∠BOE,
如图1,在△BOF中,∠AFO=∠BOF+∠B,
而∠BOE=∠BOF+∠EOF,
∴∠EOF=∠B=45°,
对图2,图3同理可证,
∴∠EOF=45°.

点E的坐标是(a,1-a),点F的坐标是(1-b,b),
当PM、PN与线段AB都相交时,如图1,
∴S△EOF=S△AOB-S△AOE-S△BOF
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| a+b-1 |
| 2 |
当PM、PN中有一条与AB相交,另一条与BA延长线或AB延长线相交时,如图2和图3,
∴S△EOF=S△FOA+S△AOE=
| 1 |
| 2 |
| 1 |
| 2 |
| a+b-1 |
| 2 |
∴S△EOF=S△FOB+S△BOE=
| 1 |
| 2 |
| 1 |
| 2 |
| a+b-1 |
| 2 |
即S△EOF=
| a+b-1 |
| 2 |
(2)△AOF和△BEO一定相似.
∵如图1,OA=OB=1,
∴∠OAF=∠EBO,
∴BE=BA-AE=
| 2 |
| (1-a)2+(1-a)2 |
| 2 |
AF=BA-BF=
| 2 |
| (1-b)2+(1-b)2 |
| 2 |
∵点P是函数y=
| 1 |
| 2x |
∴b=
| 1 |
| 2a |
∴
| 2 |
| 2 |
∴
| AF |
| OB |
| OA |
| BE |
∴△AOF∽△BEO,
∵对图2,图3同理可证,
∴△AOF∽△BEO;
(3)当点P在曲线上移动时,在△OEF中,∠EOF一定等于45°,
由(2)知,△AOF∽△BEO,
∴∠AFO=∠BOE,
如图1,在△BOF中,∠AFO=∠BOF+∠B,
而∠BOE=∠BOF+∠EOF,
∴∠EOF=∠B=45°,
对图2,图3同理可证,
∴∠EOF=45°.
点评:此题难度中等,考查反比例函数的图象和性质及相似三角形性质判定.同学们只有熟练掌握这些知识点,才能正确的解答.

练习册系列答案
相关题目
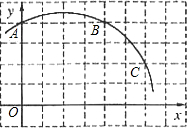 如图,已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C.
如图,已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C. 12、如图,已知直角坐标系中的点A、B的坐标分别为A(2,4)、B(4,0),且P为AB的中点.若将线段AB向右平移3个单位后,与点P对应的点为Q,则点Q的坐标是( )
12、如图,已知直角坐标系中的点A、B的坐标分别为A(2,4)、B(4,0),且P为AB的中点.若将线段AB向右平移3个单位后,与点P对应的点为Q,则点Q的坐标是( ) 7、如图,已知直角坐标系中一条圆弧经过正方形网格的格点A,B,C.若A点的坐标为(0,4),D点的坐标为(7,0),那么圆心M点的坐标( )
7、如图,已知直角坐标系中一条圆弧经过正方形网格的格点A,B,C.若A点的坐标为(0,4),D点的坐标为(7,0),那么圆心M点的坐标( )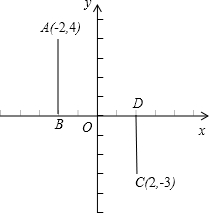 如图,已知直角坐标系中四点A(-2,4),B(-2,0),C(2,-3),D(2,0)、设P是x轴上的点,且PA、PB、AB所围成的三角形与PC、PD、CD所围成的三角形相似,请写出所有符合上述条件的点P的坐标:
如图,已知直角坐标系中四点A(-2,4),B(-2,0),C(2,-3),D(2,0)、设P是x轴上的点,且PA、PB、AB所围成的三角形与PC、PD、CD所围成的三角形相似,请写出所有符合上述条件的点P的坐标: 如图,已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C.用直尺和圆规画出该圆弧所在圆的圆心M的位置(不用写作法,保留作图痕迹).
如图,已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C.用直尺和圆规画出该圆弧所在圆的圆心M的位置(不用写作法,保留作图痕迹).