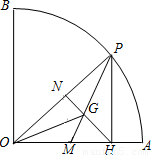摘要： 如图.在半径为9.圆心角为90°的扇形OAB的上有一动点P.PH⊥OA.垂足为H.设G为△OPH的重心(三角形的三条中线的交点).当△PHG为等腰三角形时.PH的长为 .
网址：http://m.1010jiajiao.com/timu3_id_436291[举报]
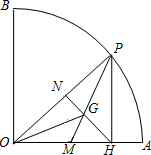如图，在半径为6，圆心角为90°的扇形OAB的弧AB上，有一个动点P，PH⊥OA，垂足为H，△PHO的中线PM与NH交于点G．（1）求证：
| PG | GM |
（2）设PH=x，GP=y，求y关于x的函数解析式，并写自变量x的取值范围；
（3）如果△PGH是等腰三角形，试求出线段PH的长． 查看习题详情和答案>>
如图，在半径为6，圆心角为90°的扇形OAB的
上，有一个动点P，PH⊥OA，垂足为H，△OPH的重心为G．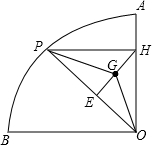
（1）设PH=x，S△PGH=y，求y关于x的函数解析式；
（2）△PGH的面积是否有最大值？如果有，求出最大面积，并求出此时PH的长度；如果没有，请说明理由；
（3）如果△PGH为等腰三角形，试求出线段PH的长． 查看习题详情和答案>>
 | AB |
（1）设PH=x，S△PGH=y，求y关于x的函数解析式；
（2）△PGH的面积是否有最大值？如果有，求出最大面积，并求出此时PH的长度；如果没有，请说明理由；
（3）如果△PGH为等腰三角形，试求出线段PH的长． 查看习题详情和答案>>
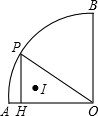如图，半径为2cm，圆心角为90°的扇形OAB的 |
| AB |
|
| AB |
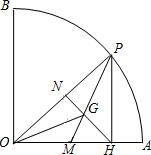如图，在半径为6，圆心角为90°的扇形OAB的弧AB上，有一个动点P，PH⊥OA，垂足为H，△PHO的中线PM与NH交于点G．
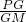=2；
=2；