题目内容
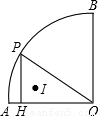
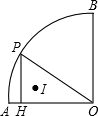 如图,半径为2cm,圆心角为90°的扇形OAB的
如图,半径为2cm,圆心角为90°的扇形OAB的 |
| AB |
 |
| AB |
分析:如图,连OI,PI,AI,由△OPH的内心为I,可得到∠PIO=180°-∠IPO-∠IOP=180°-
(∠HOP+∠OPH)=135°,并且易证△OPI≌△OAI,得到∠AIO=∠PIO=135°,所以点I在以OA为弦,并且所对的圆周角为135°的一段劣弧上;过A、I、O三点作⊙O′,如图,连O′A,O′O,在优弧AO取点P,连PA,PO,可得∠APO=180°-135°=45°,得∠AOO=90°,O′O=
OA=
×2=
,然后利用弧长公式计算弧OA的长.
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
解答: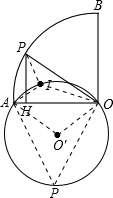 解:如图,连OI,PI,AI,
解:如图,连OI,PI,AI,
∵△OPH的内心为I,
∴∠IOP=∠IOA,∠IPO=∠IPH,
∴∠PIO=180°-∠IPO-∠IOP=180°-
(∠HOP+∠OPH),
而PH⊥OA,即∠PHO=90°,
∴∠PIO=180°-
(∠HOP+∠OPH)=180°-
(180°-90°)=135°,
又∵OP=OA,OI公共,
而∠IOP=∠IOA,
∴△OPI≌△OAI,
∴∠AIO=∠PIO=135°,
所以点I在以OA为弦,并且所对的圆周角为135°的一段劣弧上;
过A、I、O三点作⊙O′,如图,连O′A,O′O,
在优弧AO取点P,连PA,PO,
∵∠AIO=135°,
∴∠APO=180°-135°=45°,
∴∠AOO=90°,而OA=2cm,
∴O′O=
OA=
×2=
,
∴弧OA的长=
=
(cm),
所以内心I所经过的路径长为
cm.
故答案为:
cm.
 解:如图,连OI,PI,AI,
解:如图,连OI,PI,AI,∵△OPH的内心为I,
∴∠IOP=∠IOA,∠IPO=∠IPH,
∴∠PIO=180°-∠IPO-∠IOP=180°-
| 1 |
| 2 |
而PH⊥OA,即∠PHO=90°,
∴∠PIO=180°-
| 1 |
| 2 |
| 1 |
| 2 |
又∵OP=OA,OI公共,
而∠IOP=∠IOA,
∴△OPI≌△OAI,
∴∠AIO=∠PIO=135°,
所以点I在以OA为弦,并且所对的圆周角为135°的一段劣弧上;
过A、I、O三点作⊙O′,如图,连O′A,O′O,
在优弧AO取点P,连PA,PO,
∵∠AIO=135°,
∴∠APO=180°-135°=45°,
∴∠AOO=90°,而OA=2cm,
∴O′O=
| ||
| 2 |
| ||
| 2 |
| 2 |
∴弧OA的长=
90×π×
| ||
| 180 |
| ||
| 2 |
所以内心I所经过的路径长为
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题考查了弧长的计算公式:l=
,其中l表示弧长,n表示弧所对的圆心角的度数.同时考查了三角形内心的性质、三角形全等的判定与性质、圆周角定理和圆的内接四边形的性质.
| nπR |
| 180 |

练习册系列答案
相关题目
 cm的弦AB,则弦AB所对的圆心角的度数为( )
cm的弦AB,则弦AB所对的圆心角的度数为( )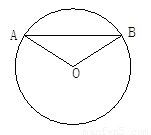
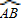 上有一运动的点P.从点P向半径OA引垂线PH交OA于点H.设△OPH的内心为I,当点P在
上有一运动的点P.从点P向半径OA引垂线PH交OA于点H.设△OPH的内心为I,当点P在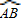 上从点A运动到点B时,内心I所经过的路径长为 .
上从点A运动到点B时,内心I所经过的路径长为 .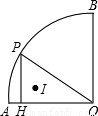
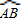 上有一运动的点P.从点P向半径OA引垂线PH交OA于点H.设△OPH的内心为I,当点P在
上有一运动的点P.从点P向半径OA引垂线PH交OA于点H.设△OPH的内心为I,当点P在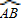 上从点A运动到点B时,内心I所经过的路径长为 .
上从点A运动到点B时,内心I所经过的路径长为 .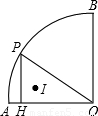
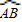 上有一运动的点P.从点P向半径OA引垂线PH交OA于点H.设△OPH的内心为I,当点P在
上有一运动的点P.从点P向半径OA引垂线PH交OA于点H.设△OPH的内心为I,当点P在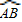 上从点A运动到点B时,内心I所经过的路径长为 .
上从点A运动到点B时,内心I所经过的路径长为 .