摘要:如图.梯形ABCD中.AD∥BC.∠DCB=45°.CD=2.BD⊥CD.过点C作CE⊥AB于E.交对角线BD于F.点G为BC中点.连接EG.AF. (1)求EG的长, (2)求证:CF=AB+AF. 考点:梯形,全等三角形的判定与性质,直角三角形斜边上的中线,勾股定理. 专题:证明题,几何综合题. 分析:(1)根据BD⊥CD.∠DCB=45°.得到∠DBC=∠DCB.求出BD=CD=2.根据勾股定理求出BC=2.根据CE⊥BE.点G为BC的中点即可求出EG, (2)在线段CF上截取CH=BA.连接DH.根据BD⊥CD.BE⊥CD.推出∠EBF=∠DCF.证出△ABD≌△HCD.得到AD=BD.∠ADB=∠HDC.根据AD∥BC.得到∠ADB=∠DBC=45°.推出∠ADB=∠HDB.证出△ADF≌△HDF.即可得到答案. 解答:(1)解:∵BD⊥CD.∠DCB=45°. ∴∠DBC=45°=∠DCB.∴BD=CD=2.在Rt△BDC中BC==2.∵CE⊥BE.点G为BC的中点.∴EG=BC=. 答:EG的长是. (2)证明:在线段CF上截取CH=BA.连接DH. ∵BD⊥CD.BE⊥CE. ∴∠EBF+∠EFB=90°.∠DFC+∠DCF=90°. ∵∠EFB=∠DFC. ∴∠EBF=∠DCF. ∵DB=CD.BA=CH. ∴△ABD≌△HCD. ∴AD=DH.∠ADB=∠HDC. ∵AD∥BC. ∴∠ADB=∠DBC=45°. ∴∠HDC=45°.∴∠HDB=∠BDC﹣∠HDC=45°. ∴∠ADB=∠HDB. ∵AD=HD.DF=DF. ∴△ADF≌△HDF. ∴AF=HF. ∴CF=CH+HF=AB+AF. ∴CF=AB+AF. 点评:本题主要考查对梯形.全等三角形的性质和判定.平行线的性质.直角三角形斜边上的中线.勾股定理等知识点的理解和掌握.综合运用性质进行推理是解此题的关键.
网址:http://m.1010jiajiao.com/timu3_id_435747[举报]
如图,梯形ABCD中,AB∥CD,AC平分∠BAD,且AC⊥BC,BC=3厘米,AC=6厘米,则△ACD的面积是( )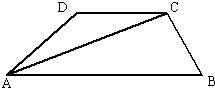

A、
| ||
| B、9平方厘米 | ||
| C、6平方厘米 | ||
| D、3平方厘米 |
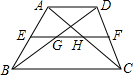 如图,梯形ABCD中,AD∥BC,EF是中位线,对角线BD、AC分别与EF相交于G、H,若GH:BC=1:3,则AD:BC的值是
如图,梯形ABCD中,AD∥BC,EF是中位线,对角线BD、AC分别与EF相交于G、H,若GH:BC=1:3,则AD:BC的值是 线段BE上取一点G,使得BF=BG,连接CG.
线段BE上取一点G,使得BF=BG,连接CG.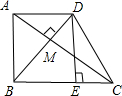 如图,梯形ABCD中,AD∥BC,对角线AC⊥BD,垂足为点M,过点D作DE⊥BC于点E,AC=8,BD=6,则梯形ABCD的高DE=
如图,梯形ABCD中,AD∥BC,对角线AC⊥BD,垂足为点M,过点D作DE⊥BC于点E,AC=8,BD=6,则梯形ABCD的高DE=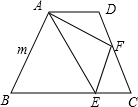 如图,梯形ABCD中,F是CD的中点,AF⊥AB,E是BC边上的一点,且AE=BE.若AB=m(m为常数),则EF的长为
如图,梯形ABCD中,F是CD的中点,AF⊥AB,E是BC边上的一点,且AE=BE.若AB=m(m为常数),则EF的长为