摘要:一个正方体物体沿斜坡向下滑动.其截面如图所示.正方形DEFH的边长为2米.坡角∠A=30°.∠B=90°.BC=6米.当正方形DEFH运动到什么位置.即当AE=米时.有DC2=AE2+BC2. 考点:一元二次方程的应用,含30度角的直角三角形,勾股定理. 分析:根据已知得出假设AE=x.可得EC=12﹣x.利用勾股定理得出DC2=DE2+EC2=4+2.AE2+BC2=x2+36.即可求出x的值. 解答:解:假设AE=x.可得EC=12﹣x. ∵坡角∠A=30°.∠B=90°.BC=6米. ∴AC=12米. ∵正方形DEFH的边长为2米.即DE=2米. ∴DC2=DE2+EC2=4+2. AE2+BC2=x2+36. ∵DC2=AE2+BC2. ∴4+2=x2+36. 解得:x=米. 故答案为:. 点评:此题主要考查了勾股定理的应用以及一元二次方程的应用.根据已知表示出CE.AE的长度是解决问题的关键.
网址:http://m.1010jiajiao.com/timu3_id_435662[举报]
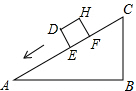 一个正方体物体沿斜坡向下滑动,其截面如图所示.正方形DEFH的边长为1米,∠B=90°,BC=4米,AC=8米,当正方形DEFH运动到什么位置时,即当AE=
一个正方体物体沿斜坡向下滑动,其截面如图所示.正方形DEFH的边长为1米,∠B=90°,BC=4米,AC=8米,当正方形DEFH运动到什么位置时,即当AE=| 49 |
| 16 |
| 49 |
| 16 |
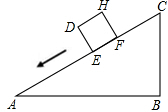 一个正方体物体沿斜坡向下滑动,其截面如图所示.正方形DEFH的边长为2米,坡角∠A=30°,∠B=90°,BC=6米.当正方形DEFH运动到什么位置,即当AE=
一个正方体物体沿斜坡向下滑动,其截面如图所示.正方形DEFH的边长为2米,坡角∠A=30°,∠B=90°,BC=6米.当正方形DEFH运动到什么位置,即当AE=
(2011•綦江县)一个正方体物体沿斜坡向下滑动,其截面如图所示.正方形DEFH的边长为2米,坡角∠A=30°,∠B=90°,BC=6米.当正方形DEFH运动到什么位置,即当AE=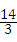 米时,有DC2=AE2+BC2.
米时,有DC2=AE2+BC2.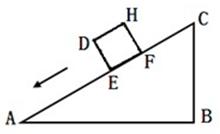 查看习题详情和答案>>
查看习题详情和答案>>
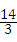 米时,有DC2=AE2+BC2.
米时,有DC2=AE2+BC2. 查看习题详情和答案>>
查看习题详情和答案>>
 米时,有DC2=AE2+BC2.
米时,有DC2=AE2+BC2.
