题目内容
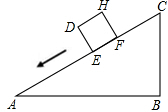 一个正方体物体沿斜坡向下滑动,其截面如图所示.正方形DEFH的边长为2米,坡角∠A=30°,∠B=90°,BC=6米.当正方形DEFH运动到什么位置,即当AE=
一个正方体物体沿斜坡向下滑动,其截面如图所示.正方形DEFH的边长为2米,坡角∠A=30°,∠B=90°,BC=6米.当正方形DEFH运动到什么位置,即当AE=分析:根据已知得出设AE=x米,可得EC=(12-x)米,利用勾股定理得出DC2=DE2+EC2=4+(12-x)2,AE2+BC2=x2+36,即可求出x的值.
解答: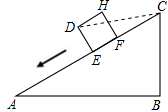 解:如图,连接CD,
解:如图,连接CD,
设AE=x米,
∵坡角∠A=30°,∠B=90°,BC=6米,
∴AC=12米,
∴EC=(12-x)米,
∵正方形DEFH的边长为2米,即DE=2米,
∴DC2=DE2+EC2=4+(12-x)2,
AE2+BC2=x2+36,
∵DC2=AE2+BC2,
∴4+(12-x)2=x2+36,
解得:x=
米.
故答案为:
.
 解:如图,连接CD,
解:如图,连接CD,设AE=x米,
∵坡角∠A=30°,∠B=90°,BC=6米,
∴AC=12米,
∴EC=(12-x)米,
∵正方形DEFH的边长为2米,即DE=2米,
∴DC2=DE2+EC2=4+(12-x)2,
AE2+BC2=x2+36,
∵DC2=AE2+BC2,
∴4+(12-x)2=x2+36,
解得:x=
| 14 |
| 3 |
故答案为:
| 14 |
| 3 |
点评:此题主要考查了勾股定理的应用以及一元二次方程的应用,根据已知表示出CE,AE的长度是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2013•南安市质检)一个正方体物体沿斜坡向上滑动,其截面如图所示,正方形DEFH的边长为1米,坡角∠A=30°,∠B=90°,BC=3米,则:
(2013•南安市质检)一个正方体物体沿斜坡向上滑动,其截面如图所示,正方形DEFH的边长为1米,坡角∠A=30°,∠B=90°,BC=3米,则: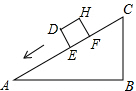 一个正方体物体沿斜坡向下滑动,其截面如图所示.正方形DEFH的边长为1米,∠B=90°,BC=4米,AC=8米,当正方形DEFH运动到什么位置时,即当AE=
一个正方体物体沿斜坡向下滑动,其截面如图所示.正方形DEFH的边长为1米,∠B=90°,BC=4米,AC=8米,当正方形DEFH运动到什么位置时,即当AE=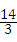 米时,有DC2=AE2+BC2.
米时,有DC2=AE2+BC2.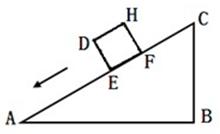
 米时,有DC2=AE2+BC2.
米时,有DC2=AE2+BC2.