摘要:在不透明的口袋中.有四个形状.大小.质地完全相同的小球.四个小球上分别标有数字.2.4.﹣.现从口袋中任取一个小球.并将该小球上的数字作为平面直角坐标系中点P的横坐标.且点P在反比例函数y=图象上.则点P落在正比例函数y=x图象上方的概率是. 考点:概率公式,正比例函数的图象,反比例函数图象上点的坐标特征. 分析:首先由点P在反比例函数y=图象上.即可求得点P的坐标.然后找到点P落在正比例函数y=x图象上方的有几个.根据概率公式求解即可. 解答:解:∵点P在反比例函数y=图象上. ∴点P的坐标可能为:(.2).(2.).(4.).(﹣.﹣3). ∵点P落在正比例函数y=x图象上方的有:(.2). ∴点P落在正比例函数y=x图象上方的概率是. 故答案为:. 点评:此题考查了反比例函数与一次函数与点的关系.以及概率公式的应用.注意概率=所求情况数与总情况数之比.
网址:http://m.1010jiajiao.com/timu3_id_435661[举报]
在不透明的口袋中,有四个形状、大小、质地完全相同的小球,四个小球上分别标有数字
,2,4,-
,现从口袋中任取一个小球,并将该小球上的数字作为平面直角坐标系中点P的横坐标,且点P在反比例函数y=
图象上,则点P落在正比例函数y=x图象上方的概率是 .
查看习题详情和答案>>
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| x |
(2011•綦江县)在不透明的口袋中,有四个形状、大小、质地完全相同的小球,四个小球上分别标有数字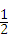 ,2,4,﹣
,2,4,﹣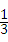 ,现从口袋中任取一个小球,并将该小球上的数字作为平面直角坐标系中点P的横坐标,且点P在反比例函数y=
,现从口袋中任取一个小球,并将该小球上的数字作为平面直角坐标系中点P的横坐标,且点P在反比例函数y=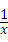 图象上,则点P落在正比例函数y=x图象上方的概率是
图象上,则点P落在正比例函数y=x图象上方的概率是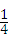 .
.
(2011•綦江县)在不透明的口袋中,有四个形状、大小、质地完全相同的小球,四个小球上分别标有数字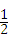 ,2,4,﹣
,2,4,﹣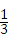 ,现从口袋中任取一个小球,并将该小球上的数字作为平面直角坐标系中点P的横坐标,且点P在反比例函数y=
,现从口袋中任取一个小球,并将该小球上的数字作为平面直角坐标系中点P的横坐标,且点P在反比例函数y=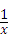 图象上,则点P落在正比例函数y=x图象上方的概率是
图象上,则点P落在正比例函数y=x图象上方的概率是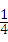 .
查看习题详情和答案>>
.
查看习题详情和答案>>
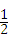 ,2,4,﹣
,2,4,﹣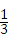 ,现从口袋中任取一个小球,并将该小球上的数字作为平面直角坐标系中点P的横坐标,且点P在反比例函数y=
,现从口袋中任取一个小球,并将该小球上的数字作为平面直角坐标系中点P的横坐标,且点P在反比例函数y=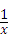 图象上,则点P落在正比例函数y=x图象上方的概率是
图象上,则点P落在正比例函数y=x图象上方的概率是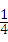 .
查看习题详情和答案>>
.
查看习题详情和答案>>
 ,2,4,-
,2,4,- ,现从口袋中任取一个小球,并将该小球上的数字作为平面直角坐标系中点P的横坐标,且点P在反比例函数y=
,现从口袋中任取一个小球,并将该小球上的数字作为平面直角坐标系中点P的横坐标,且点P在反比例函数y=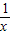 图象上,则点P落在正比例函数y=x图象上方的概率是 .
图象上,则点P落在正比例函数y=x图象上方的概率是 . ,2,4,-
,2,4,- ,现从口袋中任取一个小球,并将该小球上的数字作为平面直角坐标系中点P的横坐标,且点P在反比例函数y=
,现从口袋中任取一个小球,并将该小球上的数字作为平面直角坐标系中点P的横坐标,且点P在反比例函数y=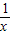 图象上,则点P落在正比例函数y=x图象上方的概率是 .
图象上,则点P落在正比例函数y=x图象上方的概率是 .