摘要：如图.PA.PB是⊙O的切线.切点是A.B.已知∠P=60°.0A=3.那么∠AOB所对弧的长度为( ) A.6π B.5π C.3π D.2π 考点:弧长的计算,切线的性质. 专题:计算题. 分析:由于PA.PB是⊙O的切线.由此得到∠OAP=∠OBP=90°.而∠P=60°.然后利用四边形的内角和即可求出∠AOB然后利用已知条件和弧长公式即可求出∠AOB所对弧的长度． 解答:解:∵PA.PB是⊙O的切线. ∴∠OAP=∠OBP=90°. 而∠P=60°. ∴∠AOB=120°. ∠AOB所对弧的长度==2π． 故选D． 点评:此题主要考查了弧长的计算问题.也利用了切线的性质和四边形的内角和.题目简单．
网址：http://m.1010jiajiao.com/timu3_id_435653[举报]
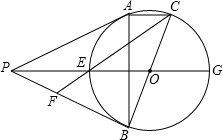如图，PA、PB是⊙0的切线，切点分别为A、B，BC是⊙0的直径，PO交⊙0于E、G两点，CE交PB于F，连AB，下列结论：①AE=CG ②AC∥PG ③PF=EF ④E为△ABP的内心，其中正确的是（ ）
查看习题详情和答案>>
19、（1）如图，在平行四边形ABCD中，∠B，∠D的平分线分别交对边于点E，F，交四边形的对角线AC于点G，H．求证：AH=CG．
（2）如图，PA，PB是⊙O的切线，点A，B为切点，AC是⊙O的直径，∠ACB=70°．求∠P的度数．
查看习题详情和答案>>
（2）如图，PA，PB是⊙O的切线，点A，B为切点，AC是⊙O的直径，∠ACB=70°．求∠P的度数．
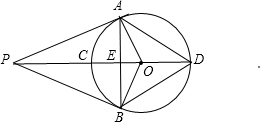
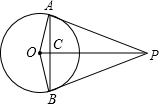（2013•永修县模拟）如图，PA、PB是⊙O的两条切线，切点分别为A、B，OP交弦AB于点C，已知sin∠APC=
如图，PA，PB是⊙O的两条切线，∠ACB=65°，则∠APB的度数为