题目内容
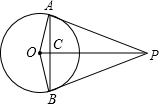（2013•永修县模拟）如图，PA、PB是⊙O的两条切线，切点分别为A、B，OP交弦AB于点C，已知sin∠APC=| 5 | 13 |
分析：由PA为圆O的切线，利用切线的性质得到三角形AOP为直角三角形，根据sin∠APC的值得出sin∠APO的值，利用锐角三角函数定义及OP的长求出OA的长，即为圆的半径．
解答：解：∵PA是圆O的两条切线，
∴∠OAP=90°，
∵sin∠APC=
，
∴sin∠APO=
=
，
∴OA=
OP=
×13=5，
则圆O的半径为5．
∴∠OAP=90°，
∵sin∠APC=
| 5 |
| 13 |
∴sin∠APO=
| OA |
| OP |
| 5 |
| 13 |
∴OA=
| 5 |
| 13 |
| 5 |
| 13 |
则圆O的半径为5．
点评：此题考查了切线的性质，以及解直角三角形，熟练掌握切线的性质是解本题的关键．
练习册系列答案
相关题目
（2013•永修县模拟）如图是五个相同的小正方体搭成的几何体，这个几何体的俯视图为（ ）