摘要: 如图,在磁感应强度B=0.3T的匀强磁场中.让导体棒PQ在U形导轨上以速度υ=10m/s向右匀速滑动.两导轨间距离L=0.5m.那么.回路中的感应电动势的大小为 .PQ中的电流方向是 (用“P→Q 或“ Q→P 表示)
网址:http://m.1010jiajiao.com/timu3_id_1628502[举报]
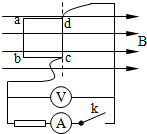 如图所示正方形线框abcd边长L=0.1m,每边电阻1Ω,在磁感应强度B=0.3T的匀强磁场中绕cd以每分钟
如图所示正方形线框abcd边长L=0.1m,每边电阻1Ω,在磁感应强度B=0.3T的匀强磁场中绕cd以每分钟2400
| ||
| π |
(1)当电键S断开时,交流电压表读数:
(2)当电键S闭合时,交流表读数.
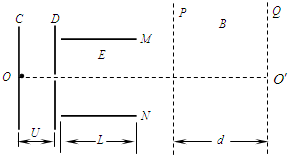 如图,某带电粒子由静止经C、D间电压U=1×103V加速后,沿两水平金属板M、N中心线OO′射入.已知两金属板长L=0.2m,板间有一沿竖直方向的匀强电场(板外无电场),场强E=1×104V/m.在板右端有一垂直纸面的匀强磁场,磁感应强度B=0.3T,P、Q是磁场的左右两个竖直理想边界,粒子在磁场中运动的最长时间为t=1.5×10-4S.(粒子重力不计,π≈3)求:
如图,某带电粒子由静止经C、D间电压U=1×103V加速后,沿两水平金属板M、N中心线OO′射入.已知两金属板长L=0.2m,板间有一沿竖直方向的匀强电场(板外无电场),场强E=1×104V/m.在板右端有一垂直纸面的匀强磁场,磁感应强度B=0.3T,P、Q是磁场的左右两个竖直理想边界,粒子在磁场中运动的最长时间为t=1.5×10-4S.(粒子重力不计,π≈3)求:(1)粒子离开偏转电场时速度方向与水平方向的夹角;
(2)粒子的比荷;
(3)磁场的最小宽度d.
如图甲所示,水平直线MN下方有竖直向上的匀强电场,其变化规律如图乙所示,电场强度E0=
V/m,现将一重力不计、比荷
=106 C/kg的带电粒子从电场中的C点由静止释放,经t1=
×10-5s的时间粒子通过MN上的D点进入匀强磁场,磁场方向垂直纸面向里,磁感应强度B按图丙所示规律变化.(计算结果均可保留π)
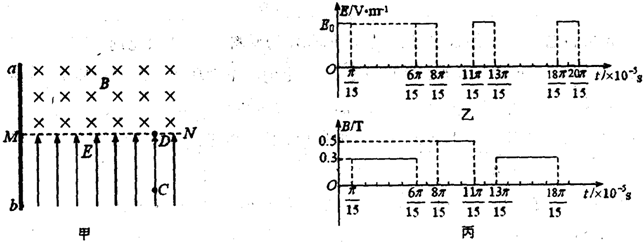
(1)求粒子到达D点时的速率;
(2)求磁感应强度Bl=0.3T时粒子做圆周运动的周期和半径;
(3)若在距D点左侧d=21cm处有一垂直于MN的足够大的挡板ab,求粒子从C点运动到挡板时所用的时间;
(4)欲使粒子垂直打在挡板ab上,求挡板ab与D点的距离所满足的条件.
查看习题详情和答案>>
| 22500 |
| π |
| q |
| m |
| π |
| 15 |

(1)求粒子到达D点时的速率;
(2)求磁感应强度Bl=0.3T时粒子做圆周运动的周期和半径;
(3)若在距D点左侧d=21cm处有一垂直于MN的足够大的挡板ab,求粒子从C点运动到挡板时所用的时间;
(4)欲使粒子垂直打在挡板ab上,求挡板ab与D点的距离所满足的条件.
 如图所示是测量通电螺线管A内部磁感应强度B及其与电流I关系的实验装置.将截面积为S、匝数为N的小试测线圈P置于螺线管A中间,试测线圈平面与螺线管的轴线垂直,可认为穿过该试测线圈的磁场均匀.将试测线圈引线的两端与冲击电流计D相连.拨动双刀双掷换向开关K,改变通入螺线管的电流方向,而不改变电流大小,在P中产生的感应电流引起D的指针偏转.
如图所示是测量通电螺线管A内部磁感应强度B及其与电流I关系的实验装置.将截面积为S、匝数为N的小试测线圈P置于螺线管A中间,试测线圈平面与螺线管的轴线垂直,可认为穿过该试测线圈的磁场均匀.将试测线圈引线的两端与冲击电流计D相连.拨动双刀双掷换向开关K,改变通入螺线管的电流方向,而不改变电流大小,在P中产生的感应电流引起D的指针偏转.(1)将开关合到位置1,待螺线管A中的电流稳定后,再将K从位置1拨到位置2,测得D的最大偏转距离为dm,已知冲击电流计的磁通灵敏度为Dφ,Dφ=
| dm |
| N△? |
(2)调节可变电阻R,多次改变电流并拨动K,得到A中电流I和磁感应强度B的数据,见右表.由此可得,螺线管A内部在感应强度B和电流I的关系为B=
| 实验次数 | I(A) | B(×10-3T) |
| 1 | 0.5 | 0.62 |
| 2 | 1.0 | 1.25 |
| 3 | 1.5 | 1.88 |
| 4 | 2.0 | 2.51 |
| 5 | 2.5 | 3.12 |
(A)适当增加试测线圈的匝数N
(B)适当增大试测线圈的横截面积S
(C)适当增大可变电阻R的阻值
(D)适当拨长拨动开关的时间△t.
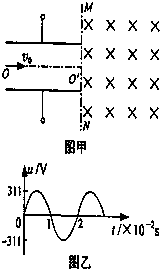 如图(甲)所示,两平行金属板间接有如图(乙)所示交变电压u,两板间电场可看作是均匀的,且两板外无电场.已知极板长L=0.2m,板间距离d=0.2m,在金属板右侧有一边界为MN的区域足够大的匀强磁场,MN与两板中线OO′垂直,磁感应强度B=5×10-3T,方向垂直纸面向里.现有带正电的粒子流沿两板中线OO′连续射入电场中,已知每个粒子的速度v0=105m/s,比荷q/m=108C/kg,
如图(甲)所示,两平行金属板间接有如图(乙)所示交变电压u,两板间电场可看作是均匀的,且两板外无电场.已知极板长L=0.2m,板间距离d=0.2m,在金属板右侧有一边界为MN的区域足够大的匀强磁场,MN与两板中线OO′垂直,磁感应强度B=5×10-3T,方向垂直纸面向里.现有带正电的粒子流沿两板中线OO′连续射入电场中,已知每个粒子的速度v0=105m/s,比荷q/m=108C/kg,不计重力,忽略粒子间的相互作用力,在每个粒子通过电场区域的极短时间内,电场可视作是恒定不变的.
(1)试求带电粒子射出电场时的最大速度.
(2)证明任意时刻从电场射出的带电粒子,进入磁场时在MN上的入射点和出磁场时在MN上的出射点间的距离为定值,写出表达式并求出这个定值.
(3)从电场射出的带电粒子,进入磁场运动一段时间后又射出磁场,求粒子在磁场中运动的最长时间.