题目内容
如图甲所示,水平直线MN下方有竖直向上的匀强电场,其变化规律如图乙所示,电场强度E0=
V/m,现将一重力不计、比荷
=106 C/kg的带电粒子从电场中的C点由静止释放,经t1=
×10-5s的时间粒子通过MN上的D点进入匀强磁场,磁场方向垂直纸面向里,磁感应强度B按图丙所示规律变化.(计算结果均可保留π)
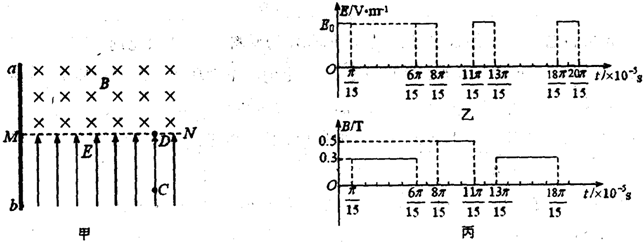
(1)求粒子到达D点时的速率;
(2)求磁感应强度Bl=0.3T时粒子做圆周运动的周期和半径;
(3)若在距D点左侧d=21cm处有一垂直于MN的足够大的挡板ab,求粒子从C点运动到挡板时所用的时间;
(4)欲使粒子垂直打在挡板ab上,求挡板ab与D点的距离所满足的条件.
| 22500 |
| π |
| q |
| m |
| π |
| 15 |

(1)求粒子到达D点时的速率;
(2)求磁感应强度Bl=0.3T时粒子做圆周运动的周期和半径;
(3)若在距D点左侧d=21cm处有一垂直于MN的足够大的挡板ab,求粒子从C点运动到挡板时所用的时间;
(4)欲使粒子垂直打在挡板ab上,求挡板ab与D点的距离所满足的条件.
分析:(1)粒子在电场中被加速运动,由运动与力的关系可求出初速度.当进入磁场时,洛伦兹力提供向心力使其做匀速圆周运动,由牛顿第二定律可算出轨道半径与周期.
(2)当粒子被电场直线加速后垂直进入磁场做半圆运动,接着又减速进入电场后再被加速进入磁场做半径不同的半圆运动,这样周而复始最终垂直打到挡板上.
(3)根据到挡板的距离可以确定完成几个周期及在电场中加速与减速的时间,最终求出总时间.
(4)粒子有可能半径大的垂直打到挡板,也可能半径小的打到板上;也可能完成
后打到挡板上,也可能完成1
,也可能更多.从而根据垂直打到挡板的要求可确定满足间距的条件.
(2)当粒子被电场直线加速后垂直进入磁场做半圆运动,接着又减速进入电场后再被加速进入磁场做半径不同的半圆运动,这样周而复始最终垂直打到挡板上.
(3)根据到挡板的距离可以确定完成几个周期及在电场中加速与减速的时间,最终求出总时间.
(4)粒子有可能半径大的垂直打到挡板,也可能半径小的打到板上;也可能完成
| 1 |
| 4 |
| 1 |
| 4 |
解答:解:(1)粒子在电场中做匀加速直线运动,则有
qE=ma
v0=at1
解得v0=1.5×104m/s
(2)设磁感应强度B1=0.3T时,粒子运动的半径为r1,运动周期为T1,
则B1qv0=m
T1=
解得r1=5cm
T1=
×10-5s
(3)设磁感应强度B2=0.5T时,粒子运动半径为r2,运动周期为T2,
则B2qv0=m
T2=
解得r2=3cm
T2=
×10-5s
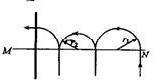
由以上计算可知,粒子的运动轨迹为如图所示的周期运动,每一个周期运动的水平距离为
S=2(r1+r2)=16cm
所以粒子运动1个整数周期后余下的距离为△d=d-s=5cm=r1
粒子从C点出发运动到挡板的时间为t=5t1+
+
+
解得t=3.24×10-5s
(4)欲使粒子垂直打在挡板ab上,挡板ab距D点的距离应满足
d=nr1+(n-1)r2
解得d=(8n-3)×10-2m(n=1,2,3,…)
或者 d=(n+1)r1+nr2
解之得 d=(8n+5)×10-2m(n=0,1,2,…)
qE=ma
v0=at1
解得v0=1.5×104m/s
(2)设磁感应强度B1=0.3T时,粒子运动的半径为r1,运动周期为T1,
则B1qv0=m
| ||
| r1 |
T1=
| 2πm |
| B1q |
解得r1=5cm
T1=
| 2π |
| 3 |
(3)设磁感应强度B2=0.5T时,粒子运动半径为r2,运动周期为T2,
则B2qv0=m
| ||
| r2 |
T2=
| 2πm |
| B2q |
解得r2=3cm
T2=
| 2π |
| 5 |
由以上计算可知,粒子的运动轨迹为如图所示的周期运动,每一个周期运动的水平距离为
S=2(r1+r2)=16cm
所以粒子运动1个整数周期后余下的距离为△d=d-s=5cm=r1
粒子从C点出发运动到挡板的时间为t=5t1+
| T1 |
| 2 |
| T2 |
| 2 |
| T1 |
| 4 |
解得t=3.24×10-5s

(4)欲使粒子垂直打在挡板ab上,挡板ab距D点的距离应满足
d=nr1+(n-1)r2
解得d=(8n-3)×10-2m(n=1,2,3,…)
或者 d=(n+1)r1+nr2
解之得 d=(8n+5)×10-2m(n=0,1,2,…)
点评:考查牛顿第二定律与运动学公式的同时,也体现了运动的重复性与周期性.注意当带电粒子在电场中加速与减速时间相等,由于洛伦兹力不做功,所以速率不变,但磁场不同,则运动半径也不同.

练习册系列答案
 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
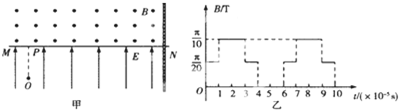






 N/C。现将一重力不计、比荷
N/C。现将一重力不计、比荷 C/kg的正电荷从电场中的O点由静止释放,经过t0=1×10-5s后,通过MN上的P点进入其上方的匀强磁场。磁场方向垂直于纸面向外,以电荷第一次通过MN时开始计时,磁感应强度按图乙所示规律周期性变化。
C/kg的正电荷从电场中的O点由静止释放,经过t0=1×10-5s后,通过MN上的P点进入其上方的匀强磁场。磁场方向垂直于纸面向外,以电荷第一次通过MN时开始计时,磁感应强度按图乙所示规律周期性变化。