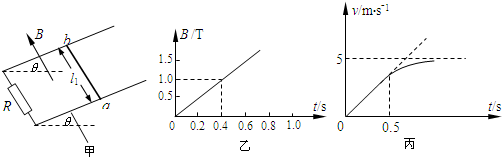
题目内容
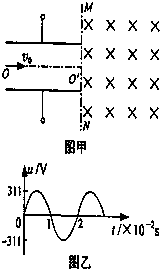 如图(甲)所示,两平行金属板间接有如图(乙)所示交变电压u,两板间电场可看作是均匀的,且两板外无电场.已知极板长L=0.2m,板间距离d=0.2m,在金属板右侧有一边界为MN的区域足够大的匀强磁场,MN与两板中线OO′垂直,磁感应强度B=5×10-3T,方向垂直纸面向里.现有带正电的粒子流沿两板中线OO′连续射入电场中,已知每个粒子的速度v0=105m/s,比荷q/m=108C/kg,
如图(甲)所示,两平行金属板间接有如图(乙)所示交变电压u,两板间电场可看作是均匀的,且两板外无电场.已知极板长L=0.2m,板间距离d=0.2m,在金属板右侧有一边界为MN的区域足够大的匀强磁场,MN与两板中线OO′垂直,磁感应强度B=5×10-3T,方向垂直纸面向里.现有带正电的粒子流沿两板中线OO′连续射入电场中,已知每个粒子的速度v0=105m/s,比荷q/m=108C/kg,不计重力,忽略粒子间的相互作用力,在每个粒子通过电场区域的极短时间内,电场可视作是恒定不变的.
(1)试求带电粒子射出电场时的最大速度.
(2)证明任意时刻从电场射出的带电粒子,进入磁场时在MN上的入射点和出磁场时在MN上的出射点间的距离为定值,写出表达式并求出这个定值.
(3)从电场射出的带电粒子,进入磁场运动一段时间后又射出磁场,求粒子在磁场中运动的最长时间.
分析:(1)粒子在电场中做类平抛运动,根据偏转的最大位移确定出偏转的最大电压,从而根据动能定理求出带电粒子射出电场时的最大速度.
(2)通过粒子进入磁场时的速度大小和方向,根据带电粒子在磁场中的半径公式,结合几何关系求出粒子从磁场中飞出的位置与进入磁场的位置之间的距离.
(3)根据几何关系求出粒子在磁场中运动的最大圆心角,从而根据周期公式求出粒子在磁场中运动的最长时间.
(2)通过粒子进入磁场时的速度大小和方向,根据带电粒子在磁场中的半径公式,结合几何关系求出粒子从磁场中飞出的位置与进入磁场的位置之间的距离.
(3)根据几何关系求出粒子在磁场中运动的最大圆心角,从而根据周期公式求出粒子在磁场中运动的最长时间.
解答:解:(1)设两板间电压为U1时,带电粒子刚好从极板边缘射出电场,则有
=
?
(
)2
代入数据得:U1=100V
当电压低于100V时,带电粒子才能从两板间射出.粒子从极板边缘射出电场时速度最大,设最大速度为v1,则有:
mv12-
mv02=q?
.
解得:v1=1.414×105m/s
(2)设某一粒子进入磁场时速度方向与OO′的夹角为θ,
则其速度大小v=
轨道半径R=
=
,
粒子从磁场中飞出的位置与进入磁场的位置之间的距离
s=2Rcosθ=
,
可见,任一带电粒子进入磁场的入射点与出射点间距为定值
将数据代入上式得s=0.4m.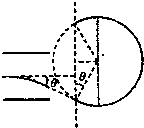
(3)设粒子飞出电场时的速度方向与OO′的最大夹角为θ,则
tanθ=
=1,所以θ=45°.
分析可知,粒子在磁场中运动的最长时间tmax=
T=
=9.42×10-6s.
答:(1)带电粒子射出电场时的最大速度为1.414×105m/s.
(2)证明如上所示.
(3)粒子在磁场中运动的最长时间为9.42×10-6s.
| d |
| 2 |
| 1 |
| 2 |
| U1q |
| dm |
| L |
| v0 |
代入数据得:U1=100V
当电压低于100V时,带电粒子才能从两板间射出.粒子从极板边缘射出电场时速度最大,设最大速度为v1,则有:
| 1 |
| 2 |
| 1 |
| 2 |
| U1 |
| 2 |
解得:v1=1.414×105m/s
(2)设某一粒子进入磁场时速度方向与OO′的夹角为θ,
则其速度大小v=
| v0 |
| cosθ |
轨道半径R=
| mv |
| qB |
| mv0 |
| qBcosθ |
粒子从磁场中飞出的位置与进入磁场的位置之间的距离
s=2Rcosθ=
| 2mv0 |
| qB |
可见,任一带电粒子进入磁场的入射点与出射点间距为定值
将数据代入上式得s=0.4m.

(3)设粒子飞出电场时的速度方向与OO′的最大夹角为θ,则
tanθ=
| ||
|
分析可知,粒子在磁场中运动的最长时间tmax=
| 3 |
| 4 |
| 3πm |
| 2qB |
答:(1)带电粒子射出电场时的最大速度为1.414×105m/s.
(2)证明如上所示.
(3)粒子在磁场中运动的最长时间为9.42×10-6s.
点评:本题关键是画出粒子进入磁场后的各种可能的运动轨迹,根据洛伦兹力提供向心力列式后得出半径和周期,然后求出磁偏转的距离表达式,并得出回旋角度的范围,从而得到磁偏转的范围和运动时间的范围.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
 在“探究平抛运动的规律”的实验中,分成两步进行:
在“探究平抛运动的规律”的实验中,分成两步进行:
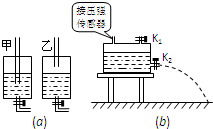 如图(a)所示,两个相同的盛水容器,密闭时装有相同水位的水.现在它们顶部各插有一根两端开口的玻璃管,甲容器中的玻璃管下端插入水中,乙容器中的玻璃管下端在水面上方.若打开容器底部的阀门,两个容器中均有水流出,在开始的一段时间内,水流出的速度不变的是
如图(a)所示,两个相同的盛水容器,密闭时装有相同水位的水.现在它们顶部各插有一根两端开口的玻璃管,甲容器中的玻璃管下端插入水中,乙容器中的玻璃管下端在水面上方.若打开容器底部的阀门,两个容器中均有水流出,在开始的一段时间内,水流出的速度不变的是