摘要:水平直导线通以恒定电流I.在其正下方有一闭合矩形线圈 abcd.线圈从静止开始释放.则线圈在下落过程中感应电流方向 是 ;下落加速度 重力加 速度.
网址:http://m.1010jiajiao.com/timu3_id_1628401[举报]
如下图,水平直导线通以恒定电流I,在其正下方有一竖直放置的闭合线圈abcd,线圈从静止开始释放,则线圈在下落过程中:
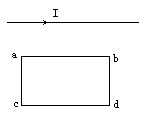
[ ]
A.没有感应电流产生
B.有电流,方向是dacba
C.下落加速度小于重力加速度
D.下落过程中,线圈机械能守恒
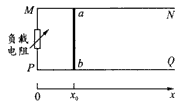
如图所示,两平行金属导轨MN、PQ被固定在同一水平面内,间距为L,电阻不计。导轨的M、P两端用直导线连结一可控的负载电阻,在PM的右侧有方向竖直向下的磁场,其磁感应强度随坐标x的变化规律为B=kx(k为正常数)。一直导体棒ab长度为L,电阻为r,其两端放在导轨上。现对导体棒持续施加一外力作用,经过很短的时间,导体棒开始以速度v沿x轴正方向匀速运动,通过调节负载电阻的阻值使通过导体棒中的电流强度I保持恒定。从导体棒匀速运动到达x=x0处开始计时,经过时间t,求(用L、k、r、v、I、x0、t表示):
(1)该时刻负载电阻消耗的电功率;
(2)时间t内负载电阻消耗的电能;
(3)时间t内回路中磁通量变化量的大小。
(1)该时刻负载电阻消耗的电功率;
(2)时间t内负载电阻消耗的电能;
(3)时间t内回路中磁通量变化量的大小。
(20)导体切割磁感线的运动可以从宏观和微观两个角度来认识。如图所示,固定于水平面的U形导线框处于竖直向下的匀强磁场中,金属直导线MN在与其垂直的水平恒力F的作用下,在导线框上以速度v做匀速运动,速度v与恒力F方向相同,导线MN始终与导线框形成闭合电路,已知导线MN电阻为R,其长度L,恰好等于平行轨道间距,磁场的磁感应强度为B,忽略摩擦阻力和导线框的电阻。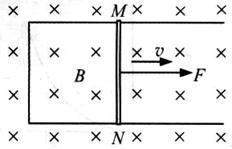
(1)通过公式推导验证:在时间内 ,F对导线MN所做的功W等于电路获得的电能
,F对导线MN所做的功W等于电路获得的电能 ,也等于导线MN中产生的焦耳热Q。
,也等于导线MN中产生的焦耳热Q。
(2)若导线的质量m=8.0g,长度L=0.1m,感应电流I=1.0A,假设一个原子贡献1个自由电子,计算导线MN中电子沿导线长度方向定向移动的平均速率v(下表中列出了一些你可能用到的数据)。
(3)经典物理学认为,金属的电阻源于定向运动自由电子和金属离子(金属原子失去电子后剩余部分)的碰撞,展开你想象的翅膀,给出一个合理的自由电子运动模型:在此基础上,求出导线MN中金属离子对一个自由电子沿导线长度方向的平均作用力 的表达式。
的表达式。
(20)导体切割磁感线的运动可以从宏观和微观两个角度来认识。如图所示,固定于水平面的U形导线框处于竖直向下的匀强磁场中,金属直导线MN在与其垂直的水平恒力F的作用下,在导线框上以速度v做匀速运动,速度v与恒力F方向相同,导线MN始终与导线框形成闭合电路,已知导线MN电阻为R,其长度L,恰好等于平行轨道间距,磁场的磁感应强度为B,忽略摩擦阻力和导线框的电阻。
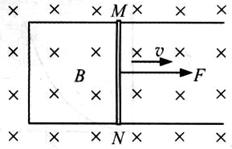
(1)通过公式推导验证:在时间内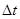 ,F对导线MN所做的功W等于电路获得的电能
,F对导线MN所做的功W等于电路获得的电能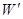 ,也等于导线MN中产生的焦耳热Q。
,也等于导线MN中产生的焦耳热Q。
(2)若导线的质量m=8.0g,长度L=0.1m,感应电流I=1.0A,假设一个原子贡献1个自由电子,计算导线MN中电子沿导线长度方向定向移动的平均速率v(下表中列出了一些你可能用到的数据)。

(3)经典物理学认为,金属的电阻源于定向运动自由电子和金属离子(金属原子失去电子后剩余部分)的碰撞,展开你想象的翅膀,给出一个合理的自由电子运动模型:在此基础上,求出导线MN中金属离子对一个自由电子沿导线长度方向的平均作用力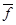 的表达式。
的表达式。

(1)通过公式推导验证:在时间内
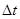 ,F对导线MN所做的功W等于电路获得的电能
,F对导线MN所做的功W等于电路获得的电能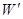 ,也等于导线MN中产生的焦耳热Q。
,也等于导线MN中产生的焦耳热Q。(2)若导线的质量m=8.0g,长度L=0.1m,感应电流I=1.0A,假设一个原子贡献1个自由电子,计算导线MN中电子沿导线长度方向定向移动的平均速率v(下表中列出了一些你可能用到的数据)。

(3)经典物理学认为,金属的电阻源于定向运动自由电子和金属离子(金属原子失去电子后剩余部分)的碰撞,展开你想象的翅膀,给出一个合理的自由电子运动模型:在此基础上,求出导线MN中金属离子对一个自由电子沿导线长度方向的平均作用力
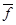 的表达式。
的表达式。 如图(甲)所示,用长度均为l的两根轻软导线水平悬吊起一质量为m、长也为l的铜棒,置于磁感应强度为B方向竖直向上的匀强磁场中.未通电时,两轻导线竖直;当通入恒定电流后,铜棒向外摆动,轻导线最大偏角为θ,求铜棒中电流的大小;
如图(甲)所示,用长度均为l的两根轻软导线水平悬吊起一质量为m、长也为l的铜棒,置于磁感应强度为B方向竖直向上的匀强磁场中.未通电时,两轻导线竖直;当通入恒定电流后,铜棒向外摆动,轻导线最大偏角为θ,求铜棒中电流的大小;