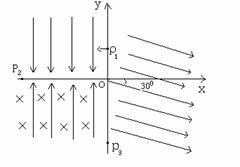
摘要：如图所示.在xy平面上.一个以原点O为中心.半径为R的圆形区域内存在着一匀强磁场.磁场的磁感应强度为B.方向垂直于xy平面向内.在O处原来静止着一个具有放射性的原子核(氮).某时刻该核发生衰变.放出一个正电子和一个反冲核.已知正电子从O点射出时沿x轴正方向.而反冲核刚好不会离开磁场区域.正电子电荷量为e.不计重力影响和粒子间的相互作用.(1)试写出的衰变方程,(2)求正电子离开磁场区域时的位置.(可能用得上的信息:碳原子序数:8)
网址：http://m.1010jiajiao.com/timu3_id_1617834[举报]
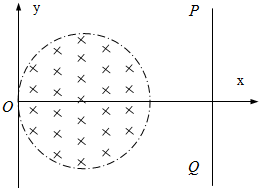如图所示，在xy平面内有一个半径为R圆形匀强磁场区域，与y轴相切于坐标原点O，磁场强度为B，方向垂直纸面向里，在x=3R处有一个与x轴垂直的荧光屏PQ，t=0时刻，在纸面内从坐标原点O以相等速率向磁场内沿不同的方向发射粒子，粒子的质量为m、电荷量为+q，其中沿x正方向发射的粒子从圆形磁场区域射出时与x轴正方向夹角为60°，粒子的重力不计．（1）求粒子的速度v0．
（2）求在磁场中运动最长时间粒子在磁场中运动的时间及此粒子打在荧光屏上的坐标（可用反三角函数表示）
（3）若虚线的圆形磁场边界是一个固定的绝缘的闭合圆环，且粒子与圆环碰撞为弹性碰撞无电荷量转移，求沿x轴正方向发射的粒子经过多长时间回到坐标原点O及粒子运动轨迹围成的面积S．
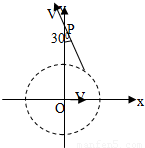
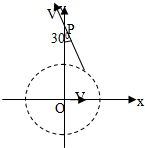如图所示，一个方向垂直于xy平面的匀强磁场磁感应强度为B，分布在以O为中心的一个圆形区域内，一个质量为m、电荷量为q的带电粒子，由原点O开始运动，初速度为v，方向沿x轴正方向．粒子经过y轴上的P点时，速度方向与y由正方向成30°角，不计重力，求和处于xy平面内磁场圆形的半径R．如图所示，一个方向垂直于xy平面的匀强磁场磁感应强度为B，分布在以O为中心的一个圆形区域内，一个质量为m、电荷量为q的带电粒子，由原点O开始运动，初速度为v，方向沿x轴正方向．粒子经过y轴上的P点时，速度方向与y由正方向成30°角，不计重力，求和处于xy平面内磁场圆形的半径R．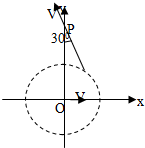
查看习题详情和答案>>
如图所示，一个方向垂直于xy平面的匀强磁场磁感应强度为B，分布在以O为中心的一个圆形区域内，一个质量为m、电荷量为q的带电粒子，由原点O开始运动，初速度为v，方向沿x轴正方向．粒子经过y轴上的P点时，速度方向与y由正方向成30°角，不计重力，求和处于xy平面内磁场圆形的半径R．
查看习题详情和答案>>
查看习题详情和答案>>
如图所示的坐标系，x轴沿水平方向，y轴沿竖直方向。在x轴上方空间的第二象限内，有一个竖直向下的匀强电场，在第三象限，存在沿y轴正方向的匀强电场和垂直xy平面（纸面）向里的匀强磁场。在第一、第四象限，存在着与x轴正方向夹角为30°的匀强电场，四个象限的电场强度大小均相等。一质量为m、电量为+q的带电质点，从y轴上y=h处的p点以一定的水平初速度沿x轴负方向进入第二象限。然后经过x轴上x=-2h处的p点进入第三象限，带电质点恰好能做匀速圆周运动。之后经过y轴上y=-2h处的p点进入第四象限。已知重力加速度为g。求：
（1）粒子到达p点时速度的大小和方向；
（2）电场强度和磁感应强度的大小；
（3）当带电质点在进入第四象限后，离x轴最近时距原点O的距离。
