题目内容
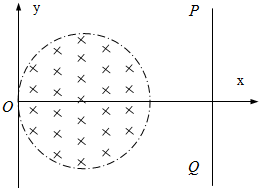 如图所示,在xy平面内有一个半径为R圆形匀强磁场区域,与y轴相切于坐标原点O,磁场强度为B,方向垂直纸面向里,在x=3R处有一个与x轴垂直的荧光屏PQ,t=0时刻,在纸面内从坐标原点O以相等速率向磁场内沿不同的方向发射粒子,粒子的质量为m、电荷量为+q,其中沿x正方向发射的粒子从圆形磁场区域射出时与x轴正方向夹角为60°,粒子的重力不计.
如图所示,在xy平面内有一个半径为R圆形匀强磁场区域,与y轴相切于坐标原点O,磁场强度为B,方向垂直纸面向里,在x=3R处有一个与x轴垂直的荧光屏PQ,t=0时刻,在纸面内从坐标原点O以相等速率向磁场内沿不同的方向发射粒子,粒子的质量为m、电荷量为+q,其中沿x正方向发射的粒子从圆形磁场区域射出时与x轴正方向夹角为60°,粒子的重力不计.(1)求粒子的速度v0.
(2)求在磁场中运动最长时间粒子在磁场中运动的时间及此粒子打在荧光屏上的坐标(可用反三角函数表示)
(3)若虚线的圆形磁场边界是一个固定的绝缘的闭合圆环,且粒子与圆环碰撞为弹性碰撞无电荷量转移,求沿x轴正方向发射的粒子经过多长时间回到坐标原点O及粒子运动轨迹围成的面积S.
分析:(1)作出粒子在磁场中运动的轨迹图,根据几何关系求出粒子在磁场中运动的轨道半径,根据洛伦兹力提供向心力求出粒子的初速度大小.
(2)当粒子在磁场中运动的轨迹弦长最长的时候,粒子运动的时间也最长,作出轨迹图,根据几何关系求出圆心角的大小,结合周期公式求出粒子在磁场中的运动时间.射出磁场后做匀速直线运动,出磁场时与x轴的夹角与进磁场时与x轴的夹角相等,根据几何关系求出粒子打在荧光屏上的坐标.
(3)作出粒子的运动轨迹图,结合圆心角,通过周期公式求出粒子在磁场中运行的时间.根据几何关系求出运动轨迹围成的面积.
(2)当粒子在磁场中运动的轨迹弦长最长的时候,粒子运动的时间也最长,作出轨迹图,根据几何关系求出圆心角的大小,结合周期公式求出粒子在磁场中的运动时间.射出磁场后做匀速直线运动,出磁场时与x轴的夹角与进磁场时与x轴的夹角相等,根据几何关系求出粒子打在荧光屏上的坐标.
(3)作出粒子的运动轨迹图,结合圆心角,通过周期公式求出粒子在磁场中运行的时间.根据几何关系求出运动轨迹围成的面积.
解答:解:(1)沿x轴正方向发射的粒子其轨迹如图,
则:r=Rcot
=
R,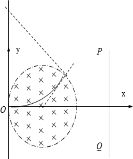
又粒子在磁场中做匀速圆周运动:qv0B=m
联立解得:v0=
.
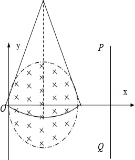
(2)因为r>R,所以当粒子在磁场中运动的轨迹弦长最长的时候,粒子运动的时间也最长,轨迹如图,设此时粒子的初始速度方向与x轴夹角为α,则:
sinα=
,又T=
=
,
所以tmax=
T=
粒子穿出磁场后做匀速运动,所以
=Rtanα=
R
所以粒子打在荧光屏的坐标为(3R,-
R)
(3)粒子的运动轨迹如图,
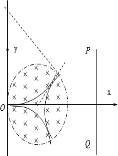
所以时间为t=3?
T=
.
所以轨迹围成的面积为
S=3(rR-
π×r2)=(3
-
)R2.
答:(1)粒子的速度v0=
.
(2)在磁场中运动最长时间粒子在磁场中运动的时间为
,粒子打在荧光屏上的坐标为(3R,-
R)
(3)沿x轴正方向发射的粒子经过
回到坐标原点O,粒子运动轨迹围成的面积为(3
-
)R2.
则:r=Rcot
| θ |
| 2 |
| 3 |

又粒子在磁场中做匀速圆周运动:qv0B=m
| v02 |
| r |
联立解得:v0=
| ||
| m |
(2)因为r>R,所以当粒子在磁场中运动的轨迹弦长最长的时候,粒子运动的时间也最长,轨迹如图,设此时粒子的初始速度方向与x轴夹角为α,则:
sinα=
| R |
| r |
| 2πr |
| v0 |
| 2πm |
| qB |

所以tmax=
| 2α |
| 2π |
2marcsin
| ||||
| Bq |
粒子穿出磁场后做匀速运动,所以
|
| ||
| 2 |
所以粒子打在荧光屏的坐标为(3R,-
| ||
| 2 |
(3)粒子的运动轨迹如图,

所以时间为t=3?
| θ |
| 2π |
| πm |
| qB |
所以轨迹围成的面积为
S=3(rR-
| θ |
| 2π |
| 3 |
| 3π |
| 2 |
答:(1)粒子的速度v0=
| ||
| m |
(2)在磁场中运动最长时间粒子在磁场中运动的时间为
2marcsin
| ||||
| Bq |
| ||
| 2 |
(3)沿x轴正方向发射的粒子经过
| πm |
| qB |
| 3 |
| 3π |
| 2 |
点评:解决本题的关键作出粒子的运动轨迹图,根据带电粒子在磁场中的半径公式、周期公式,结合几何关系进行求解.

练习册系列答案
相关题目
 (2005?南通模拟)如图所示,在xy平面内有一沿x轴正方向传播的简谐横波,波速为1m/s,振幅为4cm,频率为2.5Hz.在t=0时刻,P点位于其平衡位置上方最大位移处,则距P为0.2m的Q点( )
(2005?南通模拟)如图所示,在xy平面内有一沿x轴正方向传播的简谐横波,波速为1m/s,振幅为4cm,频率为2.5Hz.在t=0时刻,P点位于其平衡位置上方最大位移处,则距P为0.2m的Q点( )
