摘要：9．一带电粒子在如图1-26所示的点电荷的电场中.在电场力作用下沿虚线所示轨迹从A点运动到B点.电荷的加速度.动能.电势能的变化情况是( ) A．加速度的大小增大.动能.电势能都增加 B．加速度的大小减小.动能.电势能都减少 C．加速度增大.动能增加.电势能减少 D．加速度增大.动能减少.电势能增加
网址：http://m.1010jiajiao.com/timu3_id_1609497[举报]
如图所示，A板和B板为平行板电容器的两极板，其中A板带负电，B板带正电，两极板的中央都有一个小空隙可以允许粒子穿过，两板间的电势差的大小为U=1×105B极板的右上方存在着一个圆心为O1圆柱形匀强磁场区域，磁感应强度B=0.1T，磁场区域半径r=| 2 |
| 3 |
| 3 |
（1）该粒子刚刚进入圆柱形匀强磁场区域时的速度大小；
（2）该粒子通过圆形磁场区域所用的时间；
（3）该粒子在有界匀强电场中的位移大小．
如图所示，在平行板电容器的两板之间，存在相互垂直的匀强磁场和匀强电场，磁感应强度B1=0.40T，方向垂直纸面向里，电场强度E=2.0×105V/m，方向竖直向下，PQ为板间中线．紧靠平行板右侧边缘xOy坐标系的第一象限内，有一垂直纸面的矩形匀强磁场区域，磁感应强度B2=0.25T．一束带电量q=8.0×10-19C、质量m=8.0×10-26 kg的正离子从P点射入平行板间，沿中线PQ做直线运动，穿出平行板后从y轴上坐标为（0，0.2m）的Q点垂直y轴射向磁场区，粒子飞出磁场区后从A点处穿过x轴，速度方向与x轴正向夹角为θ=60°，不计离子重力，求：
（1）离子运动的速度为多大？
（2）矩形磁场区的最小面积；
（3）粒子在矩形磁场中所经历的时间．
查看习题详情和答案>>
（1）离子运动的速度为多大？
（2）矩形磁场区的最小面积；
（3）粒子在矩形磁场中所经历的时间．
如图所示，在某空间实验室中，有两个靠在一起的等大的圆柱体区域，分别存在着等大反向的匀强磁场，磁感应强度B＝0.10 T，磁场区域半径
，左侧区圆心为O1，磁场向里，右侧区圆心为O2，磁场向外，两区域切点为C，今有质量m＝3.2×10－26 kg，带电量q＝－1.6×10－19 C的某种粒子，从左侧区边缘的A点以速度v＝1.0×106 m/s沿正对O1的方向垂直射入磁场，结果它恰好穿越C点后再从右侧区穿出，求：
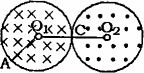
(1)请画出带电粒子在磁场中运动的轨迹图；
(2)该粒子通过两磁场区域所用的时间(结果保留三位有效数字)
如图所示在真空中XOY平面的X＞0区域内，磁感应强度B＝1.0×10－2 T的匀强磁场，方向与XOY平面垂直，在X轴上P(10 cm，0)点，有一放射源，在XOY平面内各个方向发射速度v＝1.0×105 m/s的带正电的粒子粒子质量m＝1.0×10－26 kg粒子的带电量为q＝1.0×10－18 C(重力忽略)，求：
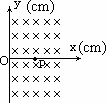
(1)带电粒子在磁场中做圆周运动的轨道半径．
(2)粒子所能到达的磁场区域的面积．
欧洲大型强子对撞机（Large Hadron Collider）简称LHC，于2009年9月重新启动，这将有望揭露自然界最基本的秘密．LHC位于瑞士、法国边境地区的地下100m深的坏形隧道中，周长26.659km（约27km）．在LHC进行的质子-质子碰撞中，每个质子的能量为7TeV（7×1012eV）．（1）目前认为，质子是由u夸克和d夸克组成，u夸克带电量为
| 2 |
| 3 |
| 1 |
| 3 |
2
2
个u夸克和1
1
个d夸克组成．（2）LHC能把数以百万计的质子加速到接近光速（光速的99.99%）．这些接近光速的质子对撞后，会创造出1百多亿年前与宇宙大爆炸之后万亿分之一秒时的状态类似的条件，科学家期望能从中发现“反物质”以及占宇宙质量96%的暗物质和暗能量的踪迹，从而揭开宇宙起源之谜．反物质是由反粒子组成，若有反α粒子，则它的质量数为
4
4
，电荷数为-2
-2
．（3）假设科学家发现了某种反粒子，采用如图的装置来测定这种反粒子的比荷（电荷量与质量之比），真空管内的K发出的反粒子（不计初速、重力和粒子间的相互作用）经加速电压加速后，穿过A'中心的小孔沿中心轴O1O的方向进入到两块水平正对放置的平行极板P和P'间的区域．当极板间不加偏转电压时，反粒子束打在荧光屏的中心O点处，形成了一个亮点；加上偏转电压U后，亮点偏离到O'点，O'与O点的竖直间距为d，水平间距可忽略不计．此时，在P和P'间的区域，再加上一个方向垂直于纸面向里的匀强磁场．调节磁场的强弱，当磁感应强度的大小为B时，亮点重新回到O点．已知极板水平方向的长度为L1，极板间距为b，极板右端到荧光屏的距离为L2（如图所示）．
①求打在荧光屏O点的反粒子速度的大小．
②推导出反粒子的比荷的表达式．