网址：http://m.1010jiajiao.com/timu3_id_1596590[举报]
如图所示，质量为M的小球被一根长为L的可绕O轴自由转动的轻质杆固定在其端点，同时又通过绳跨过光滑定滑轮与质量为m的小球相连.若将M由杆呈水平状态开始释放，不计摩擦，竖直绳足够长，则当杆转动到竖直位置时，m的速度是多大？
有一位同学的解如下：棒转到竖直位置时，M球下落距离L，绳与竖直方面成45°角，m球上升的高度为h=
L ①
设此时M球、m球的速度分别为vM、vm.有vM=vm ②
在整个运动过程中，由机械能守恒得：
MgL－mg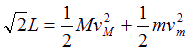
③ 由以上3式可得出m球的速度。你认为这位同学的解有没有不妥之处，如有请指出，并求出正确的结果。
如图所示，竖直面内有一个半径为R=0.2m的光滑半圆形轨道固定在地面上，水平地面与轨道相切于B点．小球以υ0=3m/s的速度从最低点B进入轨道，关于小球落地点和轨道最低点B的距离，某同学做如下计算：设小球到最高点A时的速度为υ，由机械能守恒定律：
| 1 |
| 2 |
| 1 |
| 2 |
|
小球飞行时间：t=
|
|
落地点与B点的距离：S=vt=1×0.283米=0.283米
你认为该同学的结论是否正确？如果你认为正确，请定性说明理由；如果你认为不正确，也定性说明理由（不必算出正确结果）．
某同学给出了如下的解答：
设在时间t内，床垫对运动员的平均作用力大小为F，运动员刚接触床垫时的速率为v1，刚离
开床垫时的速率为v2，则由动量定理可知Ft=△p①△p=mv2-mv1②
由机械能守恒定律分别有
| 1 |
| 2 |
| 2gh1 |
| 1 |
| 2 |
| 2gh2 |
由①②③④式联立可得 F=
m
| ||||
| t |
该同学解答过程是否正确？若不正确，请指出该同学解答过程中所有的不妥之处，并加以改正．
（2006?浦东新区一模）如图所示，质量均为m的A、B两环用细线相连后，分别套在竖直光滑细杆OQ和水平光滑细杆OP上，细线长L=1.0m．将细线拉直后使A和B在同一高度由静止释放，当A、B运动到细线与水平杆成53°角时，求A、B两环的速度vA、vB的大小．（sin53°=0.8，cos53°=0.6）；某同学求解如下：由于A、B环是系在同一根细线两端，所以它们的速度大小相等，即
vA=vB①
A环下落的高度h=Lsin53°②
由机械能守恒定律mgh=
| 1 |
| 2 |
| 1 |
| 2 |
由方程①、②、③解出vA、vB的大小即可．
问：你同意上述解题过程吗？若同意，求出vA、vB的大小；若不同意，指明错误之处并求出你认为正确的结果．
在弹性海绵垫的正上方h1高处，将重为G的小球以速率v0竖直下抛，落垫后反弹的高度为h2.设球与海绵垫第一次接触的时间为t,求在此时间内球对海绵垫的平均作用力的大小.(空气阻力不计，重力加速度为g)
吴仑同学给出了如下解答：设在时间t内海绵垫对球的平均作用力大小为F，球第一次刚接触海绵垫时的速率为v1、刚离开海绵垫时的速率为v2,则由动量定理得
Ft=Δp ①
Δp=mv2-mv1 ②
由机械能守恒定律得
mv02+mgh1=mv12 ③
mv22=mgh2 ④
由①②③④式求得F=
. ⑤
(解题过程到此结束)
试指出上述解答过程中是否有不妥之处，若有，请指出其不妥之处，并给出正确的解答.
查看习题详情和答案>>