摘要：如图所示.光滑水平面AB与竖直面内的半圆形导轨在B点衔接.导轨半径为R.一个质量为m的静止的小球在A处压缩弹簧.释放小球后.在弹簧弹力的作用下小球获得一向右的速度.当它经过B点进入导轨瞬间对导轨的压力为其重力的7倍.之后向上运动恰好能沿轨道运动到C点.求: ⑴释放小球前弹簧的弹性势能 ⑵小球由B到C克服阻力做的功 ⑶物体离开C点后落回水平面时的动能的大小 解: ⑴设小球在B处速度为v1 .小球受到支持力为FN1 有 从A到B.由功能关系得弹簧的弹性势能为: ⑵设小球在C处速度为v2 .小球受到支持力为FN2 有 小球向上运动恰好能沿轨道运动到C点.即FN2＝0 .故 设小球从B到C.克服阻力做功为Wf .则根据动能定理有: 解得: ⑶设物体离开C点后落回水平面时的动能为Ek 则根据动能定理有: 解得:
网址：http://m.1010jiajiao.com/timu3_id_1595941[举报]
如图所示，光滑水平面AB与竖直面内的半圆形导轨在B点衔接，导轨半径为R，一个质量为m的小球将弹簧压缩至A处．小球从A处由静止释放被弹开后，经过B点进入导轨瞬间对导轨的压力为其重力的8倍，之后向上运动恰能沿轨道运动到C点，求：（1）释放小球前弹簧的弹性势能．
（2）小球由B到C克服阻力做的功．
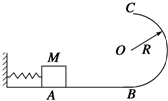如图所示，光滑水平面AB与竖直面内的半圆形导轨在B点衔接，导轨半径为R，一个质量为m的静止物块在A处压缩弹簧，在弹力的作用下获得某一向右速度，当它经过B点进入导轨瞬间对导轨的压力为其重力的7倍，之后向上运动恰能完成半圆周运动到达C点．求：（1）弹簧对物体的弹力做的功？
（2）物块从B至C克服阻力做的功？
如图所示，光滑水平面AB与竖直面内的半圆形导轨在B点相接，导轨半径为R．一个质量为m的物体将弹簧压缩至A点后由静止释放，在弹力作用下物体获得某一向右速度后脱离弹簧，当它经过B点进入导轨瞬间对导轨的压力为其重力的7倍，之后向上运动恰能完成半个圆周运动到达C点．不计空气阻力．试求：
（1）当m在A点时，弹簧的弹性势能的大小；
（2）物块m从B点运动到C点克服阻力做的功的大小；
（3）如果半圆形轨道也是光滑的，其他条件不变，当物体由A经B运动到C，然后落到水平面，落点为D（题中D点未标出，且水平面足够长），求D点与B点间距离．
如图所示，光滑水平面AB与竖直面内的半圆形导轨在B点相接，导轨半径为R．一个质量为m的物体将弹簧压缩至A点后由静止释放，在弹力作用下物体获得某一向右速度后脱离弹簧，当它经过B点进入导轨瞬间对导轨的压力为其重力的7倍，之后向上运动恰能完成半个圆周运动到达C点．试求：