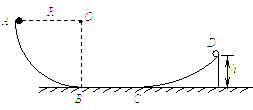摘要:20.如图所示.AB为固定在竖直平面内的四分之一光滑圆弧轨道.轨道的B点与水平地面相切.其半径为R.质量为m的小球由A点静止释放.求: (1)小球滑到最低点B时.小球速度v的大小, (2)小球通过光滑水平面BC滑上固定曲面.恰达最高点D. 且D到地面的高度为h(已知h<R).则小球在曲面上 克服摩擦力所做的功为多大?
网址:http://m.1010jiajiao.com/timu3_id_1576412[举报]
 如图所示,AB为固定在竖直平面内的
如图所示,AB为固定在竖直平面内的| 1 | 4 |
(1)小球滑到最低点B时,小球速度v的大小;
(2)小球通过光滑的水平面BC滑上固定曲面,恰达最高点D,D到地面的高度为h(已知h<R),则小球在曲面上克服摩擦力所做的功Wf.
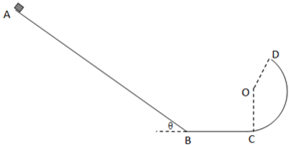 如图所示,AB为固定在竖直平面内粗糙倾斜轨道,BC为光滑水平轨道,CD为固定在竖直平面内的光滑圆弧轨道,且AB与BC通过一小段光滑弧形轨道相连,BC与弧CD相切.已知AB长为L=10m,倾角θ=37°,BC长s=4m,CD弧的半径为R=2m,O为其圆心,∠COD=143°.整个装置处在水平向左的匀强电场中,电场强度大小为E=1×103N/C.一质量为m=0.4kg、电荷量为q=+3×10-3C的物体从A点以初速度vA=15m/s沿AB轨道开始运动.若物体与轨道AB间的动摩擦因数为μ=0.2,sin37°=0.6,cos37°=0.8,g=10m/s2,物体运动过程中电荷量不变.求:
如图所示,AB为固定在竖直平面内粗糙倾斜轨道,BC为光滑水平轨道,CD为固定在竖直平面内的光滑圆弧轨道,且AB与BC通过一小段光滑弧形轨道相连,BC与弧CD相切.已知AB长为L=10m,倾角θ=37°,BC长s=4m,CD弧的半径为R=2m,O为其圆心,∠COD=143°.整个装置处在水平向左的匀强电场中,电场强度大小为E=1×103N/C.一质量为m=0.4kg、电荷量为q=+3×10-3C的物体从A点以初速度vA=15m/s沿AB轨道开始运动.若物体与轨道AB间的动摩擦因数为μ=0.2,sin37°=0.6,cos37°=0.8,g=10m/s2,物体运动过程中电荷量不变.求:(1)物体在AB轨道上运动时,重力和电场力对物体所做的总功;
(2)物体到达B点的速度;
(3)通过计算说明物体能否到达D点.
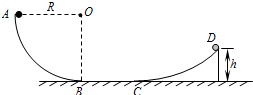 如图所示,AB为固定在竖直平面内的
如图所示,AB为固定在竖直平面内的| 1 | 4 |
(1)小球滑到最低点B时,小球速度v的大小;
(2)小球刚到达最低点B时,轨道对小球支持力FN的大小;
(3)小球通过光滑的水平面BC滑上固定曲面,恰达最高点D,D到地面的高度为h(已知h<R),则小球在曲面上克服摩擦力所做的功Wf.
如图所示,AB为固定在竖直平面内粗糙倾斜轨道,BC为光滑水平轨道,CD为固定在竖直平面内的光滑圆弧轨道,且AB与BC通过一小段光滑弧形轨道相连,BC与弧CD相切.已知AB长为L=10m,倾角θ=37°,BC长s=
m,CD弧的半径为R=
m,O为其圆心,∠COD=143°.整个装置处在水平向左的匀强电场中,电场强度大小为E=1×103N/C.一质量为m=0.4kg、电荷量为q=+3×10 -3C的物体从A点以初速度vA=15m/s沿AB轨道开始运动.若物体与轨道AB间的动摩擦因数为μ=0.2,sin37°=0.6,cos37°=0.8,g=10m/s2,物体运动过程中电荷量不变.求
(1)物体在AB轨道上运动时,重力和电场力对物体所做的总功;
(2)物体能否到达D点;
(3)物体离开CD轨道后运动的最高点相对于O点的水平距离x和竖直距离y.

查看习题详情和答案>>
| 35 |
| 9 |
| 25 |
| 12 |
(1)物体在AB轨道上运动时,重力和电场力对物体所做的总功;
(2)物体能否到达D点;
(3)物体离开CD轨道后运动的最高点相对于O点的水平距离x和竖直距离y.