题目内容
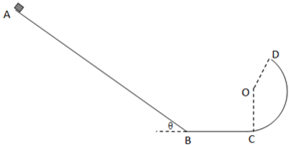 如图所示,AB为固定在竖直平面内粗糙倾斜轨道,BC为光滑水平轨道,CD为固定在竖直平面内的光滑圆弧轨道,且AB与BC通过一小段光滑弧形轨道相连,BC与弧CD相切.已知AB长为L=10m,倾角θ=37°,BC长s=4m,CD弧的半径为R=2m,O为其圆心,∠COD=143°.整个装置处在水平向左的匀强电场中,电场强度大小为E=1×103N/C.一质量为m=0.4kg、电荷量为q=+3×10-3C的物体从A点以初速度vA=15m/s沿AB轨道开始运动.若物体与轨道AB间的动摩擦因数为μ=0.2,sin37°=0.6,cos37°=0.8,g=10m/s2,物体运动过程中电荷量不变.求:
如图所示,AB为固定在竖直平面内粗糙倾斜轨道,BC为光滑水平轨道,CD为固定在竖直平面内的光滑圆弧轨道,且AB与BC通过一小段光滑弧形轨道相连,BC与弧CD相切.已知AB长为L=10m,倾角θ=37°,BC长s=4m,CD弧的半径为R=2m,O为其圆心,∠COD=143°.整个装置处在水平向左的匀强电场中,电场强度大小为E=1×103N/C.一质量为m=0.4kg、电荷量为q=+3×10-3C的物体从A点以初速度vA=15m/s沿AB轨道开始运动.若物体与轨道AB间的动摩擦因数为μ=0.2,sin37°=0.6,cos37°=0.8,g=10m/s2,物体运动过程中电荷量不变.求:(1)物体在AB轨道上运动时,重力和电场力对物体所做的总功;
(2)物体到达B点的速度;
(3)通过计算说明物体能否到达D点.
分析:(1)小球带正电,而电场水平向左,故电场力水平向左,与重力垂直,求合力的功,可先求合力再求功,也可以分别求功再加代数和
(2)应用动能定理求解速度
(3)设物体能到D点,对物体由A到D的过程,由动能定理求出物体到达D点的速度,与恰好到达D处的临界速度比较,分析能否到达D点;
(2)应用动能定理求解速度
(3)设物体能到D点,对物体由A到D的过程,由动能定理求出物体到达D点的速度,与恰好到达D处的临界速度比较,分析能否到达D点;
解答:解:(1)物体所受重力和电场力的合力大小为F=
=5N
合力与竖直方向的夹角为α,则:
sinα=
=
得:α=37°
即合力与轨道AB垂直,所以物体在轨道AB上运动时重力和电场力对物体做的总功为W=0
(2)在AB段上物体所受摩擦力:f=μF=1N
对AB段运动使用动能定理:-fL=
m
-
m
解得:vB=5
m/s
(3)D点为CD轨道上的等效最高点,设物体能到D点,其速度为vD
对物体由B到D的过程由动能定理得:
-qE(s+Rsinα)-mg(R+Rcosα)=
m
-
m
解得:vD=5m/s
设物体恰能到D点时速度为v0,由牛顿第二定律得:F=
解得v0=5m/s
故v0=vD
因此物体恰好能到达D点
答:(1)物体在AB轨道上运动时,重力和电场力对物体所做的总功为0
(2)物体到达B点的速度为5
m/s
(3)通过计算物体能到达D点.
| (mg)2+(qE)2 |
合力与竖直方向的夹角为α,则:
sinα=
| qE |
| F |
| 3 |
| 5 |
得:α=37°
即合力与轨道AB垂直,所以物体在轨道AB上运动时重力和电场力对物体做的总功为W=0
(2)在AB段上物体所受摩擦力:f=μF=1N
对AB段运动使用动能定理:-fL=
| 1 |
| 2 |
| v | 2 B |
| 1 |
| 2 |
| v | 2 A |
解得:vB=5
| 7 |
(3)D点为CD轨道上的等效最高点,设物体能到D点,其速度为vD
对物体由B到D的过程由动能定理得:
-qE(s+Rsinα)-mg(R+Rcosα)=
| 1 |
| 2 |
| v | 2 D |
| 1 |
| 2 |
| v | 2 B |
解得:vD=5m/s
设物体恰能到D点时速度为v0,由牛顿第二定律得:F=
m
| ||
| R |
解得v0=5m/s
故v0=vD
因此物体恰好能到达D点
答:(1)物体在AB轨道上运动时,重力和电场力对物体所做的总功为0
(2)物体到达B点的速度为5
| 7 |
(3)通过计算物体能到达D点.
点评:本题运用牛顿第二定律和运动学公式结合研究带电体在电场力和重力场的复合场中运动问题,难点是确定物体离开轨道的位置,抓住此时轨道的弹力为零,由牛顿第二定律研究

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案
相关题目
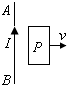 如图所示,AB为固定的通电直导线,闭合导线框P与AB在同一平面内.当P远离AB做匀速运动时,它受到AB的作用力为( )
如图所示,AB为固定的通电直导线,闭合导线框P与AB在同一平面内.当P远离AB做匀速运动时,它受到AB的作用力为( ) 如图所示,AB为固定在竖直平面内的
如图所示,AB为固定在竖直平面内的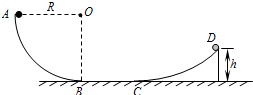 如图所示,AB为固定在竖直平面内的
如图所示,AB为固定在竖直平面内的