摘要:如图8-1所示.质量为m=0.4kg的滑块.在水平外力F作用下.在光滑水平面上从A点由静止开始向B点运动.到达B点时外力F突然撤去.滑块随即冲上半径为 R=0.4米的1/4光滑圆弧面小车.小车立即沿光滑水平面PQ运动.设:开始时平面AB与圆弧CD相切.A.B.C三点在同一水平线上.令AB连线为X轴.且AB=d=0.64m.滑块在AB面上运动时.其动量随位移的变化关系为P=1.6kgm/s.小车质量M=3.6kg.不计能量损失.求:(1)滑块受水平推力F为多大? (2)滑块通过C点时.圆弧C点受到压力为多大? (3)滑块到达D点时.小车速度为多大? (4)滑块能否第二次通过C点? 若滑块第二次通过C点时.小车与滑块的速度分别为多大? (5)滑块从D点滑出再返回D点这一过程中.小车移动距离为多少? (g取10m/s2) 分析与解:(1)由P=1.6=mv.代入x=0.64m.可得滑块到B点速度为: VB=1.6/m=1.6=3.2m/s A→B.由动能定理得:FS=mVB2 所以 F=mVB2/(2S)=0.4X3.22/滑块滑上C立即做圆周运动.由牛顿第二定律得: N-mg=mVC2/R 而VC=VB 则 N=mg+mVC2/R=0.4X10+0.4X3.22/0.4=14.2N (3)滑块由C→D的过程中.滑块和小车组成系统在水平方向动量守恒.由于滑块始终紧贴着小车一起运动.在D点时.滑块和小车具有相同的水平速度VDX .由动量守恒定律得:mVC=(M+m)VDX 所以 VDX=mVC/(M+m)=0.4X3.2/=0.32m/s (4)滑块一定能再次通过C点.因为滑块到达D点时.除与小车有相同的水平速度VDX外.还具有竖直向上的分速度VDY.因此滑块以后将脱离小车相对于小车做竖直上抛运动.因题中说明无能量损失.可知滑块在离车后一段时间内.始终处于D点的正上方(因两者在水平方向不受力作用.水平方向分运动为匀速运动.具有相同水平速度). 所以滑块返回时必重新落在小车的D点上.然后再圆孤下滑.最后由C点离开小车.做平抛运动落到地面上.由机械能守恒定律得: mVC2=mgR+(M+m)VDX2+mVDY2 所以 以滑块.小车为系统.以滑块滑上C点为初态.滑块第二次滑到C点时为末态.此过程中系统水平方向动量守恒.系统机械能守恒(注意:对滑块来说.此过程中弹力与速度不垂直.弹力做功.机械能不守恒)得: mVC=mVC'+MV 即mVC2=mVC'2+MV2 上式中VC'.V分别为滑块返回C点时.滑块与小车的速度. V=2mVC/(M+m)=2X0.4X3.2/=0.64m/s VC'=(m-M)VC/X3.2/=-2.56m/s滑块离D到返回D这一过程中.小车做匀速直线运动.前进距离为: △S=VDX2VDY/g=0.32X2X1.1/10=0.07m
网址:http://m.1010jiajiao.com/timu3_id_1548923[举报]
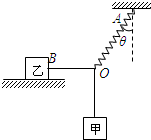
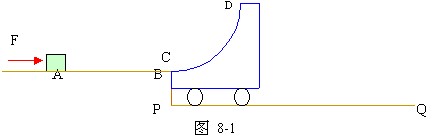
如图8-1所示,质量为m=0.4kg的滑块,在水平外力F作用下,在光滑水平面上从A点由静止开始向B点运动,到达B点时外力F突然撤去,滑块随即冲上半径为 R=0.4米的1/4光滑圆弧面小车,小车立即沿光滑水平面PQ运动。设:开始时平面AB与圆弧CD相切,A、B、C三点在同一水平线上,令AB连线为X轴,且AB=d=0.64m,滑块在AB面上运动时,其动量随位移的变化关系为P=1.6![]() kgm/s,小车质量M=3.6kg,不计能量损失。求:
kgm/s,小车质量M=3.6kg,不计能量损失。求:
(1)滑块受水平推力F为多大? (2)滑块通过C点时,圆弧C点受到压力为多大? (3)滑块到达D点时,小车速度为多大? (4)滑块能否第二次通过C点? 若滑块第二次通过C点时,小车与滑块的速度分别为多大? (5)滑块从D点滑出再返回D点这一过程中,小车移动距离为多少? (g取10m/s2)
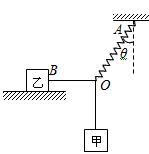
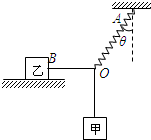 如图所示,质量为m1=0.4Kg的物体甲通过二段轻绳和一个轻质细弹簧悬挂在结点O.轻绳OB水平且B端与放置在水平面上质量为m2=0.5Kg的物体乙相连,轻弹簧OA与竖直方向的夹角θ=370,物体甲、乙均处于静止状态.(已知:sin37°=0.6,cos37°=0.8,tan37°=0.75;g取10m/s2.)求:
如图所示,质量为m1=0.4Kg的物体甲通过二段轻绳和一个轻质细弹簧悬挂在结点O.轻绳OB水平且B端与放置在水平面上质量为m2=0.5Kg的物体乙相连,轻弹簧OA与竖直方向的夹角θ=370,物体甲、乙均处于静止状态.(已知:sin37°=0.6,cos37°=0.8,tan37°=0.75;g取10m/s2.)求:(1)若轻弹簧的劲度系数为K=500N/m,则轻弹簧的伸长长度是多大?
(2)物体乙受到的摩擦力是多大?方向如何?
(3)若物体乙的最大静摩擦力等于12N,则欲使物体乙在水平面上不滑动,物体甲的质量m1最大不能超过多少?(将AO替换为细绳,保持O点位置不变)
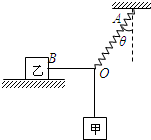 如图所示,质量为m1=0.4Kg的物体甲通过二段轻绳和一个轻质细弹簧悬挂在结点O.轻绳OB水平且B端与放置在水平面上质量为m2=0.5Kg的物体乙相连,轻弹簧OA与竖直方向的夹角θ=370,物体甲、乙均处于静止状态.(已知:sin37°=0.6,cos37°=0.8,tan37°=0.75;g取10m/s2.)求:
如图所示,质量为m1=0.4Kg的物体甲通过二段轻绳和一个轻质细弹簧悬挂在结点O.轻绳OB水平且B端与放置在水平面上质量为m2=0.5Kg的物体乙相连,轻弹簧OA与竖直方向的夹角θ=370,物体甲、乙均处于静止状态.(已知:sin37°=0.6,cos37°=0.8,tan37°=0.75;g取10m/s2.)求: