摘要:如图所示.一质量为M的平板车B放在光滑水平面上.在其右端放一质量为m的小木块A.已知m<M.A.B间动摩擦因数为μ.现给A和B以大小相等.方向相反的初速度v0.使A开始向左运动.B开始向右运动.最后A不会滑离B.求: (1)A.B最后的速度大小和方向. (2)从地面上看.小木块向左运动到离出发点最远处时.平板车向右运动的位移大小. 解析:(1)A不会滑离B板.说明A.B具有相同的速度.设此速度为v. A和B的初速度的大小为v0.则据动量守恒定律可得: Mv0-mv0=(M+m)v 解得:v=v0.方向向右. (2)从地面上看.小木块向左运动到离出发点最远处时.木块速度为零.平板车速度为v′.由动量守恒定律得: Mv0-mv0=Mv′ 设这一过程平板向右运动距离s.则有: μmgs=Mv-Mv′2 解得s=v. 答案:(1)v0.方向向右 (2)v
网址:http://m.1010jiajiao.com/timu3_id_1386306[举报]
 如图所示,一质量为M的平板车B放在光滑水平面上,在其右端放一质量为m的小木块A,M=3m,A、B间动摩擦因数为μ,现给A和B以大小相等、方向相反的初速度v0,使A开始向左运动,B开始向右运动,最后A不会滑离B,求:
如图所示,一质量为M的平板车B放在光滑水平面上,在其右端放一质量为m的小木块A,M=3m,A、B间动摩擦因数为μ,现给A和B以大小相等、方向相反的初速度v0,使A开始向左运动,B开始向右运动,最后A不会滑离B,求:①A、B最后的速度大小和方向;
②要使A最终不脱离B,平板车B的最短长度为多少
③从地面上看,小木块向左运动到离出发点最远处时,平板车向右运动的位移大小.
 如图所示,一质量为M的平板车B放在光滑水平面上,在其右端放一质量为m的小木块A,m<M,A、B间动摩擦因数为μ,现给A和B以大小相等、方向相反的初速度v0,使A开始向左运动,B开始向右运动,最后A不会滑离B,求:
如图所示,一质量为M的平板车B放在光滑水平面上,在其右端放一质量为m的小木块A,m<M,A、B间动摩擦因数为μ,现给A和B以大小相等、方向相反的初速度v0,使A开始向左运动,B开始向右运动,最后A不会滑离B,求:(1)A、B最后的速度大小和方向.
(2)从地面上看,小木块向左运动到离出发点最远处时,平板车向右运动的位移大小.
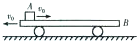 如图所示,一质量为M的平板车B放在光滑水平面上,在其左端放一质量为m的小木块A,m<M,A、B间动摩擦因数为μ,现同时给A和B大小相等、方向相反的初速度v0,使A开始向右运动,B开始向左运动,最后A不会滑离B.求:
如图所示,一质量为M的平板车B放在光滑水平面上,在其左端放一质量为m的小木块A,m<M,A、B间动摩擦因数为μ,现同时给A和B大小相等、方向相反的初速度v0,使A开始向右运动,B开始向左运动,最后A不会滑离B.求:(1)A、B最后的速度大小和方向;
(2)A在B上相对滑动的时间.

