摘要:证明:正整数列是常数列的充要条件是其满足性质p:对数列中任意2n项,存在一种方法将这2n项分为两类,使得两类数之和相等. 物理 题型分值
网址:http://m.1010jiajiao.com/timu3_id_1301959[举报]
数列{an}前n项和为Sn,首项为x(x∈R),满足Sn=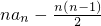 (n∈N*)
(n∈N*)
(1)求数列{an}的通项公式;
(2)是否存在x(x∈R),使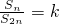 (其中k是与正整数n无关的常数),若存在,求出x与k的值,若不存在,说明理由;
(其中k是与正整数n无关的常数),若存在,求出x与k的值,若不存在,说明理由;
(3)求证:x为有理数的充要条件是数列{an}中存在三项构成等比数列.
查看习题详情和答案>>
数列{an}前n项和为Sn,首项为x(x∈R),满足Sn=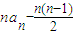 (n∈N*)
(n∈N*)
(1)求数列{an}的通项公式;
(2)是否存在x(x∈R),使 (其中k是与正整数n无关的常数),若存在,求出x与k的值,若不存在,说明理由;
(其中k是与正整数n无关的常数),若存在,求出x与k的值,若不存在,说明理由;
(3)求证:x为有理数的充要条件是数列{an}中存在三项构成等比数列.
查看习题详情和答案>>
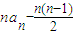 (n∈N*)
(n∈N*)(1)求数列{an}的通项公式;
(2)是否存在x(x∈R),使
 (其中k是与正整数n无关的常数),若存在,求出x与k的值,若不存在,说明理由;
(其中k是与正整数n无关的常数),若存在,求出x与k的值,若不存在,说明理由;(3)求证:x为有理数的充要条件是数列{an}中存在三项构成等比数列.
查看习题详情和答案>>
数列{an}前n项和为Sn,首项为x(x∈R),满足Sn=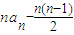 (n∈N*)
(n∈N*)
(1)求数列{an}的通项公式;
(2)是否存在x(x∈R),使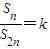 (其中k是与正整数n无关的常数),若存在,求出x与k的值,若不存在,说明理由;
(其中k是与正整数n无关的常数),若存在,求出x与k的值,若不存在,说明理由;
(3)求证:x为有理数的充要条件是数列{an}中存在三项构成等比数列.
查看习题详情和答案>>
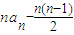 (n∈N*)
(n∈N*)(1)求数列{an}的通项公式;
(2)是否存在x(x∈R),使
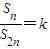 (其中k是与正整数n无关的常数),若存在,求出x与k的值,若不存在,说明理由;
(其中k是与正整数n无关的常数),若存在,求出x与k的值,若不存在,说明理由;(3)求证:x为有理数的充要条件是数列{an}中存在三项构成等比数列.
查看习题详情和答案>>
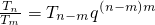 (q>0是常数).
(q>0是常数).