题目内容
数列{an}前n项和为Sn,首项为x(x∈R),满足Sn=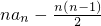 (n∈N*)
(n∈N*)
(1)求数列{an}的通项公式;
(2)是否存在x(x∈R),使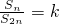 (其中k是与正整数n无关的常数),若存在,求出x与k的值,若不存在,说明理由;
(其中k是与正整数n无关的常数),若存在,求出x与k的值,若不存在,说明理由;
(3)求证:x为有理数的充要条件是数列{an}中存在三项构成等比数列.
解:由Sn=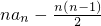 (n∈N*)得由Sn+1=
(n∈N*)得由Sn+1=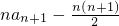
故可得an+1=(n+1)an+1-nan-n∴an+1-an=1,即数列{an}是等差数列,首项为x公差为1,∴an=x+(n-1)(n∈N*)
(2)由题意Sn=kS2n,即xn+ n(n-1)=k(2xn+n(2n-1)),整理得(1-4k)n-(2x-1)(2k-1)=0,当x=
n(n-1)=k(2xn+n(2n-1)),整理得(1-4k)n-(2x-1)(2k-1)=0,当x= ,k=
,k= 时,该式恒成立即:当x=
时,该式恒成立即:当x= 时,
时,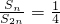 ,∴x=
,∴x= ,k=
,k= 即为所求
即为所求
(3))证明:充分性若三个不同的项x+i,x+j,x+k成等比数列,且i<j<k
则(x+j)2=(x+i)(x+k),即x(i+k-2j)=j2-ik
若i+k-2j=0,则j2-ik=0,∴i=j=k与i<j<k矛盾.i+k-2j≠0
∴x=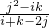 ,且i,j,k都是非负数,∴x是有理数;
,且i,j,k都是非负数,∴x是有理数;
必要性:若x是有理数,且x≤0,则必存在正整数k,使x+k>0,令y=x+k,则正项数列y,y+1,y+2…是原数列
x,x+1,x+2…的一个子数列,只要正项数列y,y+1,y+2…中存在三个不同的项构成等比数列则原数列中必有3个不同项构成等比数列,
不失一般性,不妨设x>0,记x= (m,n∈N*,且m,b互质),又设k,l∈N*,l>k,且x,x+k,x+l成等比数列,则(x+k)2=x(x+l)?2k+
(m,n∈N*,且m,b互质),又设k,l∈N*,l>k,且x,x+k,x+l成等比数列,则(x+k)2=x(x+l)?2k+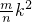 ,为使l为整数,可令k=2n,于是l=2n+mn=n(m+2),可知x,x+n,x+n(m+2),成等比数列,证毕
,为使l为整数,可令k=2n,于是l=2n+mn=n(m+2),可知x,x+n,x+n(m+2),成等比数列,证毕
分析:(1)由Sn=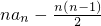 (n∈N*)得由Sn+1=
(n∈N*)得由Sn+1=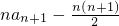 ,由此两方程得出an+1-an=1,即数列{an}是等差数列,由等差数列的通项公式写出数列的通项;
,由此两方程得出an+1-an=1,即数列{an}是等差数列,由等差数列的通项公式写出数列的通项;
(2)假设存在,由题意Sn=kS2n,即xn+ n(n-1)=k(2xn+n(2n-1)),整理得(1-4k)n-(2x-1)(2k-1)=0进行判断即可得到x与k的值
n(n-1)=k(2xn+n(2n-1)),整理得(1-4k)n-(2x-1)(2k-1)=0进行判断即可得到x与k的值
(3)由充要条件的证明方法,先证充分性,再证必要性即可.
点评:本题考查数列的递推式,解题的关键是充分利用递推式的恒成立的特性,通过恒等变形得到数列的性质,从而求出数列的通项,本题第三问涉及到了充要条件的证明,要注意其证明格式.本题比较抽象,运算量大,运算变形时要认真严谨.
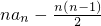 (n∈N*)得由Sn+1=
(n∈N*)得由Sn+1=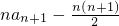
故可得an+1=(n+1)an+1-nan-n∴an+1-an=1,即数列{an}是等差数列,首项为x公差为1,∴an=x+(n-1)(n∈N*)
(2)由题意Sn=kS2n,即xn+
 n(n-1)=k(2xn+n(2n-1)),整理得(1-4k)n-(2x-1)(2k-1)=0,当x=
n(n-1)=k(2xn+n(2n-1)),整理得(1-4k)n-(2x-1)(2k-1)=0,当x= ,k=
,k= 时,该式恒成立即:当x=
时,该式恒成立即:当x= 时,
时,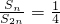 ,∴x=
,∴x= ,k=
,k= 即为所求
即为所求(3))证明:充分性若三个不同的项x+i,x+j,x+k成等比数列,且i<j<k
则(x+j)2=(x+i)(x+k),即x(i+k-2j)=j2-ik
若i+k-2j=0,则j2-ik=0,∴i=j=k与i<j<k矛盾.i+k-2j≠0
∴x=
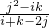 ,且i,j,k都是非负数,∴x是有理数;
,且i,j,k都是非负数,∴x是有理数;必要性:若x是有理数,且x≤0,则必存在正整数k,使x+k>0,令y=x+k,则正项数列y,y+1,y+2…是原数列
x,x+1,x+2…的一个子数列,只要正项数列y,y+1,y+2…中存在三个不同的项构成等比数列则原数列中必有3个不同项构成等比数列,
不失一般性,不妨设x>0,记x=
 (m,n∈N*,且m,b互质),又设k,l∈N*,l>k,且x,x+k,x+l成等比数列,则(x+k)2=x(x+l)?2k+
(m,n∈N*,且m,b互质),又设k,l∈N*,l>k,且x,x+k,x+l成等比数列,则(x+k)2=x(x+l)?2k+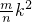 ,为使l为整数,可令k=2n,于是l=2n+mn=n(m+2),可知x,x+n,x+n(m+2),成等比数列,证毕
,为使l为整数,可令k=2n,于是l=2n+mn=n(m+2),可知x,x+n,x+n(m+2),成等比数列,证毕分析:(1)由Sn=
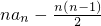 (n∈N*)得由Sn+1=
(n∈N*)得由Sn+1=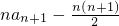 ,由此两方程得出an+1-an=1,即数列{an}是等差数列,由等差数列的通项公式写出数列的通项;
,由此两方程得出an+1-an=1,即数列{an}是等差数列,由等差数列的通项公式写出数列的通项;(2)假设存在,由题意Sn=kS2n,即xn+
 n(n-1)=k(2xn+n(2n-1)),整理得(1-4k)n-(2x-1)(2k-1)=0进行判断即可得到x与k的值
n(n-1)=k(2xn+n(2n-1)),整理得(1-4k)n-(2x-1)(2k-1)=0进行判断即可得到x与k的值(3)由充要条件的证明方法,先证充分性,再证必要性即可.
点评:本题考查数列的递推式,解题的关键是充分利用递推式的恒成立的特性,通过恒等变形得到数列的性质,从而求出数列的通项,本题第三问涉及到了充要条件的证明,要注意其证明格式.本题比较抽象,运算量大,运算变形时要认真严谨.

练习册系列答案
相关题目