摘要：如图13所示.在光滑绝缘的水平面上.用长为2L的绝缘轻杆连接两个质量均为m的带电小球A和B.A球的电荷量为+2q.B球的电荷量为-3q.组成一静止的带电系统.虚线NQ与MP平行且相距3L.开始时MP恰为杆的中垂线.视小球为质点.不计轻杆的质量.现在在虚线MP.NQ间加上水平向右的匀强电场E.求: (1)B球刚进入电场时带电系统的速度大小, (2)B球的最大位移以及从开始到最大位移处时B球电势能的变化量, (3)带电系统运动的周期.
网址：http://m.1010jiajiao.com/timu3_id_1237051[举报]
如图13所示，在光滑水平面上的O点系一长为l的绝缘细线，线的另一端系一质量为m、带电荷量为q的小球.当沿细线方向加上场强为E的匀强电场后，小球处于平衡状态.现给小球一垂直于细线的初速度v0，使小球在水平面上开始运动.若v0很小，则小球再次回到平衡位置所需的时间为（ ）?
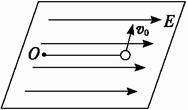
图13
A.
B.
C.
D.
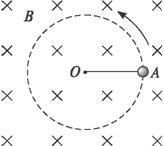
如图13-1-5所示，在光滑绝缘的水平面上的A、B两点分别放置质量为m和2m的两个点电荷QA和QB.将两个点电荷同时释放，已知刚释放时QA的加速度为a，经过一段时间后(两电荷未相遇)，QB的加速度也为a，且此时QB的速度大小为v.求：
(1)此时QA的速度和加速度各多大？
(2)这段时间内QA和QB构成的系统增加的动能.
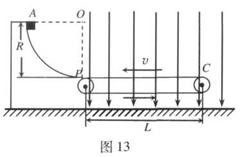
查看习题详情和答案>>如图13所示，四分之一光滑绝缘圆弧轨道AP和水平绝缘传送带PC固定在同一 竖直平面内，圆弧轨道的圆心为0，半径为R0传送带PC之间的距离为L,沿逆时针方向 的运动速度v=
.在PO的右侧空间存在方向竖直向下的匀强电场。一质量为m、电荷量 为+q的小物体从圆弧顶点A由静止开始沿轨 道下滑，恰好运动到C端后返回。物体与传送 带间的动摩擦因数为
，不计物体经过轨道与传 送带连接处P时的机械能损失,重力加速度为g
(1) 求物体下滑到P点时，物体对轨道的压力F
(2) 求物体返回到圆弧轨道后，能上升的最大高度H
(3) 若在PO的右侧空间再加上方向垂直于纸面向里、磁感应强度为B的水平匀强磁场 (图中未画出），物体从圆弧顶点A静止释放,运动到C端时的速度为
，试求物体 在传送带上运动的时间t。
查看习题详情和答案>>
如图甲所示，一足够长阻值不计的光滑平行金属导轨MN、PQ之间的距离L=1.0m，NQ两端连接阻值R=3.0Ω的电阻，磁感应强度为B的匀强磁场垂直于导轨所在平面向上，导轨平面与水平面间的夹角θ=300．一质量m=0.20kg，阻值r=0.50Ω的金属棒垂直于导轨放置并用绝缘细线通过光滑的定滑轮与质量M=0.60kg的重物相连．细线与金属导轨平行．金属棒沿导轨向上滑行的速度v与时间t之间的关系如图乙所示，已知金属棒在0～0.3s内通过的电量是0.3～0.6s内通过电量的