成都市2006年高中阶段教育学校统一招生考试试卷(北师大版)
A卷(共100分)
一、选择题:(每小题3分,共30分)
1、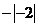 的倒数是( )
的倒数是( )
A、2 B、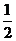 C、
C、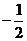 D、-2
D、-2
2、2007年中国月球探测工程的“嫦娥一号”卫星将发射升空飞向月球。已知地球距离月球表面约为384000千米,那么这个距离用科学记数法(保留三个有效数字)表示应为( )
A、3.84×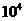 千米 B、3.84×
千米 B、3.84× 千米 C、3.84×
千米 C、3.84×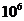 千米 D、38.4×
千米 D、38.4×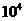 千米
千米
 3、右图是由一些完全相同的小立方块搭成的几何体的三种视图,那么搭成这个几何体所用的小立方块的个数是( )
3、右图是由一些完全相同的小立方块搭成的几何体的三种视图,那么搭成这个几何体所用的小立方块的个数是( )
A、5个 B、6个 C、7个 D、8个
4、下列运算正确的是( )
A、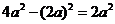 B、
B、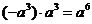 C、
C、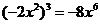 D、
D、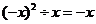
5、下列事件中,不可能事件是( )
A、掷一枚六个面分别刻有1~6数码的均匀正方体骰子。向上一面的点数是“5”
B、任意选择某个电视频道,正在播放动画片
C、肥皂泡会破碎
D、在平面内,度量一个三角形的内角度数,其和为360°
6 、已知代数式 与
与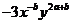 是同类项,那么a、b的值分别是( )
是同类项,那么a、b的值分别是( )
 A、
A、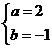 B、
B、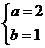 C、
C、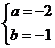 D、
D、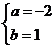
7、把一张长方形的纸片按如图所示的方式折叠,EM、FM为折痕,折叠后的C点落在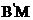 或
或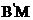 的延长线上,那么∠EMF的度数是( )
的延长线上,那么∠EMF的度数是( )
A、85° B、90° C、95° D、100°
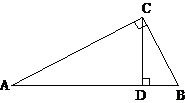 8、如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D。已知AC=
8、如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D。已知AC= ,BC=2,那么sin∠ACD=( )
,BC=2,那么sin∠ACD=( )
 A、
A、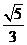 B、
B、 C、
C、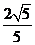 D、
D、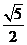
9、为了了解汽车司机遵守交通法规的意识,小明的学习小组成员协助交通警察在某路口统计的某个时段来往汽车的车速(单位:千米/小时)情况如图所示。根据统计图分析,这组车速数据的众数和中位数分别是( )
A、60千米/小时,60千米/小时
B、58千米/小时,60千米/小时
C、60千米/小时,58千米/小时
D、58千米/小时,58千米/小时
 10、如图,小丽要制作一个圆锥模型,要求圆锥的母线长为9cm,底面圆的直径为10cm,那么小丽要制作的这个圆锥的侧面展开扇形的纸片的圆心角度数是( )
10、如图,小丽要制作一个圆锥模型,要求圆锥的母线长为9cm,底面圆的直径为10cm,那么小丽要制作的这个圆锥的侧面展开扇形的纸片的圆心角度数是( )
A、150° B、200° C、180° D、240°
将答案直接写在该题目中的横线上。
二、填空题:(每小题4分,共20分)
11、把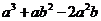 分解因式的结果是______________。
分解因式的结果是______________。
 12、函数
12、函数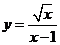 的自变量x的取值范围是______________。
的自变量x的取值范围是______________。
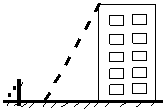
13、如图,小华为了测量所住楼房的高度,他请来同学帮忙,测量了同一时刻他自己的影长和楼房的影长分别是0.5米和15米。已知小华的身高为1.6米,那么他所住楼房的高度为________米。
 14、如图,在等腰梯形ABCD中,AD∥BC,AB≠AD,对角线AC、BD相交于点O。如下四个结论:
14、如图,在等腰梯形ABCD中,AD∥BC,AB≠AD,对角线AC、BD相交于点O。如下四个结论:
① 梯形ABCD是轴对称图形;②∠DAC=∠DCA;
② △AOB≌△DOC;④△AOD∽△BOC
请把其中正确结论的序号填在横线上:______________。
 15、右图表示甲骑电动自行车和乙驾驶汽车沿相同的路线行驶45千米,由A地到B地时,行驶的路程y(千米)与经过的时间x(小时)之间的函数关系。请根据这个行驶过程中的图象填空:汽车出发_____小时与电动自行车相遇;电动自行车的速度为_____千米/小时;汽车的速度为_____千米/小时;汽车比电动自行车早_____小时到达B地。
15、右图表示甲骑电动自行车和乙驾驶汽车沿相同的路线行驶45千米,由A地到B地时,行驶的路程y(千米)与经过的时间x(小时)之间的函数关系。请根据这个行驶过程中的图象填空:汽车出发_____小时与电动自行车相遇;电动自行车的速度为_____千米/小时;汽车的速度为_____千米/小时;汽车比电动自行车早_____小时到达B地。
三、(共18分)
16、解答下列各题:(每小题6分)
(1) 计算: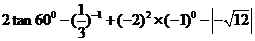
(2) 先化简,再求值: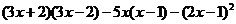 ,其中
,其中
(3) 解方程: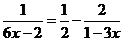
四、(每小题8分,共16分)
17、如图,方格纸中的每个小方格都是边长为1的正方形,我们把以格点间连线为边的三角形称为“格点三角形”,图中的△ABC就是格点三角形。在建立平面直角坐标系后,点B的坐标为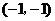 。
。
(1) 把△ABC向左平移8格后得到△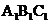 ,画出△
,画出△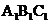 的图形并写出点
的图形并写出点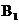 的坐标;
的坐标;
(2) 把△ABC绕点C按顺时针方向旋转90°后得到△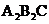 ,画出△
,画出△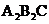 的图形并写出点
的图形并写出点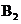 的坐标;
的坐标;
(3) 把△ABC以点A为位似中心放大,使放大前后对应边长的比为1:2,画出△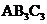

18、小明、小芳做一个“配色”的游戏,右图是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形,并涂上图中所示的颜色。同时转动两个转盘,如果转盘A转出红色,转盘B转出蓝色,或者转盘A转出了蓝色,转盘B转出了红色,则红色和蓝色在一起配成紫色,这种情况下小芳获胜;同样,蓝色和黄色在一起配成绿色,这种情况下小明获胜;在其它情况下,则小明、小芳不分胜负。
(4) 利用列表或树状图的方法表示此游戏所有可能出现的结果;
(5) 此游戏的规则,对小明、小芳公平吗?试说明理由。
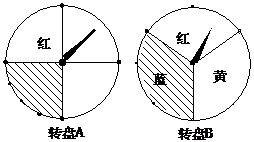
二、(每小题8分,共16分)
19、已知:如图,在△ABC中,D是AC的中点,E是线段BC延长线一点,过点A作BE的平行线与线段ED的延长线交于点F,连结AE、CF。
(6) 求证:AF=CE;
(7) 若AC=EF,试判断四边形AFCE是什么样的四边形,并证明你的结论。

20、如图,已知反比例函数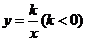 的图象经过点A
的图象经过点A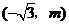 ,过点A作AB⊥x轴于点B,且△AOB的面积为
,过点A作AB⊥x轴于点B,且△AOB的面积为 。
。
(1) 求k和m的值;
(2)  若一次函数
若一次函数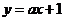 的图象经过点A,并且与x轴相交于点C,求∠ACO的度数和
的图象经过点A,并且与x轴相交于点C,求∠ACO的度数和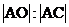 的值。
的值。
B卷(共50分)
将答案直接写在该题目中的横线上。
一、填空题:(每小题4分,共20分)
21、不等式组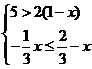 的整数解的和是______________。
的整数解的和是______________。
22、含有4种花色的36张扑克牌的牌面都朝下,每次抽出一张记下花色后再原样放回,洗匀牌后再抽。不断重复上述过程,记录抽到红心的频率为25%,那么其中扑克牌花色是红心的大约有______________张。
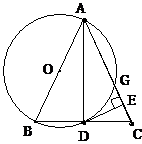 23、如图,以等腰三角形ABC的一腰AB为直径的⊙O交BC于点D,交AC于点G,连结AD,并过点D作DE⊥AC,垂足为E。根据以上条件写出三个正确结论(除AB=AC、AO=BO、∠ABC=∠ACB外)是:
23、如图,以等腰三角形ABC的一腰AB为直径的⊙O交BC于点D,交AC于点G,连结AD,并过点D作DE⊥AC,垂足为E。根据以上条件写出三个正确结论(除AB=AC、AO=BO、∠ABC=∠ACB外)是:
(1)______________
(2)______________
(3)______________
24、已知某工厂计划经过两年的时间,把某种产品从现在的年产量100万台提高到121万台,那么每年平均增长的百分数是______________。按此年平均增长率,预计第4年该工厂的年产量应为______________万台。
25、如图,如果以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去,…,已知正方形ABCD的面积 为1,按上述方法所作的正方形的面积依次为
为1,按上述方法所作的正方形的面积依次为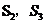 ,…,
,…,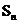 (n为正整数),那么第8个正方形的面积
(n为正整数),那么第8个正方形的面积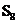 =_______。
=_______。

二、(共8分)
26、如图,某校九年级3班的一个学习小组进行测量小山高度的实践活动。部分同学在山脚点A测得山腰上一点D的仰角为30°,并测得AD的长度为180米;另一部分同学在山顶点B测得山脚点A的俯角为45°,山腰点D的俯角为60°。请你帮助他们计算出小山的高度BC(计算过程和结果都不取近似值)。
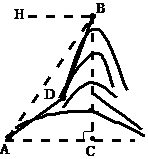
三、(共10分)
(邛崃、大邑、新津、浦江四市、县的考生不做,其余考生做)
27、已知:如图,⊙O与⊙A相交于C、D两点,A、O分别是两圆的圆心,△ABC内接于⊙O,弦CD交AB于点G,交⊙O的直径AE于点F,连结BD。
(1) 求证:△ACG∽△DBG;
(2)
求证: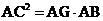 ;
;
(3)
若⊙A、⊙O的直径分别为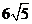 、15,且CG:CD=1:4,求AB和BD的长。
、15,且CG:CD=1:4,求AB和BD的长。
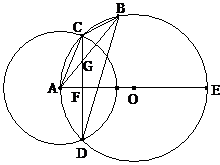
(邛崃、大邑、新津、浦江四市、县的考生做,其余考生不做)
27、已知:如图,在正方形ABCD中,AD=12,点E是边CD上的动点(点E不与端点C、D重合),AE的垂直平分线FP分别交AD、AE、BC于点F、H、G,交AB的延长线于点P。
(1)
设DE=m(0<m<12),试用含m的代数式表示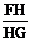 的值;
的值;
(2)
在(1)的条件下,当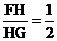 时,求BP的长。
时,求BP的长。
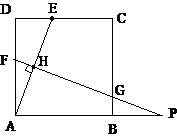
四、(共12分)
28、如图,在平面直角坐标系中,已知点B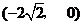 ,A
,A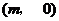
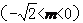 ,以AB为边在x轴下方作正方形ABCD,点E是线段OD与正方形ABCD的外接圆除点D以外的另一个交点,连结BE与AD相交于点F。
,以AB为边在x轴下方作正方形ABCD,点E是线段OD与正方形ABCD的外接圆除点D以外的另一个交点,连结BE与AD相交于点F。
(1) 求证:BF=DO;
(2) 设直线l是△BDO的边BO的垂直平分线,且与BE相交于点G,若G是△BDO的外心,试求经过B、F、O三点的抛物线的解析式;
(3) 在(2)的条件下,在抛物线上是否存在点P,使该点关于直线BE的对称点在x轴上?若存在,求出所有这样的点的坐标;若不存在,请说明理由。
