摘要:(2) 在(1)的条件下.当时.求BP的长.
网址:http://m.1010jiajiao.com/timu_id_8235[举报]
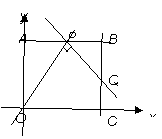
如图,在平面直角坐标系中,四边形OABC为矩形,OA=3,OC=4,P为直线AB上一动点,将直线OP绕点P逆时针方向旋转90°交直线BC于点Q;
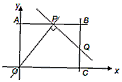
(1)当点P在线段AB上运动(不与A,B重合)时,求证:OA·BQ=AP·BP;
(2)在(1)成立的条件下,设点P的横坐标为m,线段CQ的长度为l,求出l关于m的函数解析式,并判断l是否存在最小值,若存在,请求出最小值;若不存在,请说明理由;
(3)直线AB上是否存在点P,使△POQ为等腰三角形,若存在,请求出点P的坐标;若不存在,请说明理由。
查看习题详情和答案>>
(2)在(1)成立的条件下,设点P的横坐标为m,线段CQ的长度为l,求出l关于m的函数解析式,并判断l是否存在最小值,若存在,请求出最小值;若不存在,请说明理由;
(3)直线AB上是否存在点P,使△POQ为等腰三角形,若存在,请求出点P的坐标;若不存在,请说明理由。
已知:点P为正方形ABCD内部一点,且∠BPC=900,过点P的直线分别交边AB、边CD于
点E、点F.
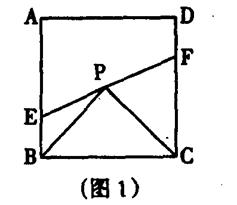
(1)如图l,当PC=PB时,则S△PBE、S△PCF S△BPC之间的数量关系为
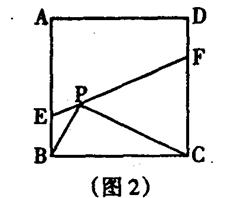
(2)如图2,当PC=2PB时,求证:16S△PBE+S△PCF =4S△BP
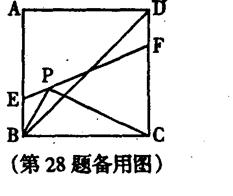
. (3)在(2)的条件下,Q为AD边上一点,且∠PQF=900,连接BD,BD交QF于点N,若S△bpc =80,
BE=6。求线段DN的长.
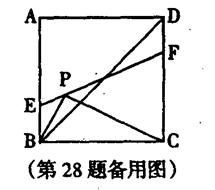
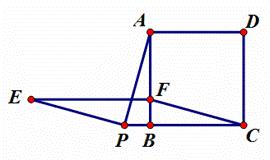
如图,正方形ABCD的边长是3,点P是直线BC上一点,连接PA,将线段PA绕点P逆时针旋转![]() 得到线段PE,在直线BA上取点F,使BF=BP,且点F与点E在BC同侧,连接EF,CF.
得到线段PE,在直线BA上取点F,使BF=BP,且点F与点E在BC同侧,连接EF,CF.
⑴如图,当点P在CB延长线上时,求证:四边形PCFE是平行四边形;
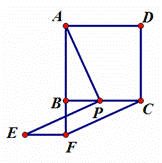
⑵如图‚,当点P在线段BC上时,四边形PCFE是否还是平行四边形,说明理由;
⑶在⑵的条件下,四边形PCFE的面积是否有最大值?若有,请求出面积的最大值及此时BP长;若没有,请说明理由。
|
第25题 图 |
第25题 图‚ |
 (3)直线
(3)直线