北京市东城区2008――2009学年度
高二年级数学选修课程模块1-2测试题(文科卷)
一、选择题:本大题共12小题.每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.在复平面内,复数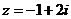 对应的点位于( )
对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.两个形状一样的杯子 和
和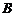 中分别装有红葡萄酒和白葡萄酒.现在利用空杯子
中分别装有红葡萄酒和白葡萄酒.现在利用空杯子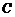 将
将 和
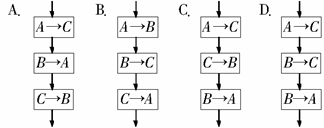
和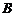 两个杯子里所装的酒对调,下面画出的流程图正确的是( )
两个杯子里所装的酒对调,下面画出的流程图正确的是( )
3.计算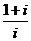 的结果是( )
的结果是( )
A.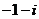 B.
B.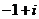 C.
C.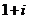 D.
D.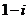
4.由直线与圆相切时,圆心到切点连线与直线垂直,想到平面与球相切时,球心与切点连线与平面垂直,用的是( )
A.归纳推理 B.演绎推理 C.类比推理 D.其它推理
5. 在线性回归模型 中,下列说法正确的是 ( )
中,下列说法正确的是 ( )
A. 是一次函数
是一次函数
B.因变量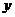 是由自变量
是由自变量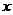 唯一确定的
唯一确定的
C.随机误差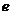 是由于计算不准确造成的,可以通过精确计算避免随机误差e的产生
是由于计算不准确造成的,可以通过精确计算避免随机误差e的产生
D.因变量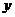 除了受自变量
除了受自变量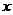 的影响外,可能还受到其它因素的影响,这些因素会导致随机误差
的影响外,可能还受到其它因素的影响,这些因素会导致随机误差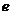 的产生
的产生
6. 类比“等差数列的定义”给出一个新数列“等和数列的定义”是( )
A.连续两项的和相等的数列叫等和数列
B.从第二项起,以后每一项与前一项的差都不相等的数列叫等和数列
C.从第二项起,以后每一项与前一项的和都相等的数列叫等和数列
D.从第一项起,以后每一项与前一项的和都相等的数列叫等和数列
7.在建立两个变量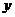 与
与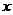 的回归模型中,分别选择了4个不同模型,他们的相关指数
的回归模型中,分别选择了4个不同模型,他们的相关指数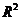 如下,其中拟合的最好的模型是( )
如下,其中拟合的最好的模型是( )
A.模型1的相关指数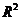 为
为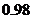 B.模型2的相关指数
B.模型2的相关指数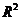 为
为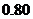
C.模型3的相关指数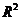 为
为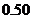 D.模型4的相关指数
D.模型4的相关指数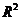 为
为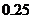
 8.图中所示的是一个算法的流程图.
8.图中所示的是一个算法的流程图.
已知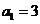 ,输出的结果为
,输出的结果为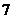 ,
,
则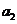 的值为(
)
的值为(
)
A.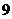
B.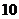
C.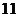
D.
9.有一段演绎推理是这样的:“直线平行于平面,则此直线平行于平面内的所有直线;已知直线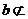 平面
平面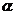 ,直线
,直线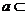 平面
平面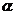 ,直线
,直线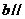 平面
平面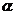 ,则直线
,则直线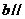 直线
直线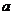 ” .结论显然是错误的,这是因为( )
” .结论显然是错误的,这是因为( )
A.推理形式错误 B.大前提错误 C.小前提错误 D.非以上错误
10. 在研究某新措施对“非典”的防治效果问题时,得到如下列联表:
存活数
死亡数
合计
新措施
132
18
150
对照
114
36
150
合计
246
54
300
由表中数据可得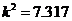 ,故我们由此认为 “新措施对防治非典有效” 的把握为( )
,故我们由此认为 “新措施对防治非典有效” 的把握为( )
A.0 B.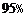 C.
C.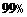 D.
D.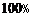
11. 下面几种推理过程是演绎推理的是( )
A.两条直线平行,同旁内角互补,如果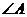 与
与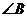 是两条平行直线的同旁内角,则
是两条平行直线的同旁内角,则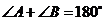
B.某校高二(1)班有55人,高二(2)班有52人,由此得高二所有班人数超过50人
C.由平面三角形的性质,推出空间四边形的性质
D.在数列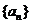 中,
中,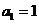 ,
,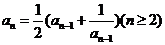 ,通过计算
,通过计算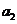 ,
,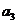 ,
,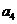 由此归纳出
由此归纳出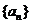 的通项公式
的通项公式
12.已知数列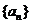 满足
满足 ,
,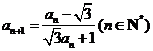 ,则
,则 等于( )
等于( )
A.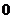 B.
B.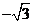 C.
C.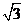 D.
D.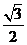
二、填空题:本大题共4小题,每小题4分,共16分.将答案填在题中横线上.
13. 若复数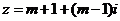 为纯虚数,则实数
为纯虚数,则实数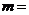 ____________.
____________.
14. 现有爬行、哺乳、飞行三类动物,其中蛇、地龟属于爬行动物;狼、狗属于哺乳动物;鹰、长尾雀属于飞行动物,请你把下列结构图补充完整.

15. 用演绎法证明 在区间
在区间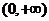 为增函数时的大前提是
.
为增函数时的大前提是
.
16.在平面,到一条直线的距离等于定长(为正数)的点的集合是与该直线平行的两条直线.这一结论推广到空间则为:在空间,到一个平面的距离等于定长的点的集合是 .
三、解答题:本大题共3小题,共36分. 解答应写出文字说明、证明过程或演算步骤.
17. (本小题满分12分)
在关于人体脂肪含量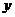 (百分比)和年龄
(百分比)和年龄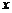 关系的研究中,得到如下一组数据
关系的研究中,得到如下一组数据
年龄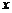
23
27
39
41
45
50
脂肪含量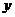
9.5
17.8
21.2
25.9
27.5
28.2
(Ⅰ)画出散点图,判断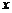 与
与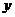 是否具有相关关系;
是否具有相关关系;
(Ⅱ)通过计算可知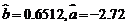 ,请写出
,请写出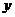 对
对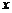 的回归直线方程,并计算出
的回归直线方程,并计算出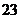 岁和
岁和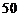 岁的残差.
岁的残差.
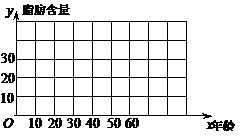
求证: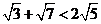 .
.
18B. (本小题满分12分)
已知函数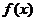 是
是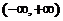 上的增函数,
上的增函数,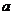 ,
,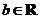 .
.
(Ⅰ)若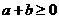 ,求证:
,求证: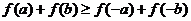 ;
;
(Ⅱ)判断(Ⅰ)中命题的逆命题是否成立,并证明你的结论.
数列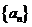 满足
满足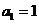 ,
,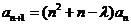 (
(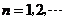 ),
),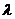 是常数.
是常数.
(Ⅰ)当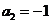 时,求
时,求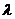 及
及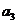 的值;
的值;
(Ⅱ)数列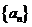 是否可能为等差数列?若可能,求出它的通项公式;若不可能,说明理由.
是否可能为等差数列?若可能,求出它的通项公式;若不可能,说明理由.
19B. (本小题满分12分)
设数列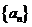 的首项
的首项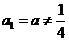 ,且
,且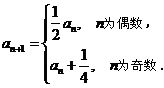 记
记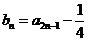 ,
,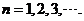
(Ⅰ)求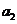 ,
,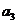 ,
,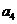 ,
,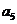 ;
;
(Ⅱ)判断数列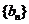 是否为等比数列,并证明你的判断.
是否为等比数列,并证明你的判断.
北京市东城区2008――2009学年度
高二年级数学选修课程模块1-2测试题(文科卷)
一、选择题(本大题共12小题,每小题4分,共48分)
1.B 2.A 3.D 4.C 5.D 6.C
7.A 8.C 9.B 10.C 11.A 12.B
二、填空题(本大题共4小题,每小题4分,共16分)
13. 
14. 
15. 增函数的定义
16. 与该平面平行的两个平面
三、解答题(本大题共3小题,每小题12分,共36分)
17.(本小题满分12分)
 解:(Ⅰ)涉及两个变量,年龄与脂肪含量.
解:(Ⅰ)涉及两个变量,年龄与脂肪含量.
因此选取年龄为自变量 ,脂肪含量为因变量
,脂肪含量为因变量 .
.
作散点图,从图中可看出 与
与 具有相关关系.
具有相关关系.
┄┄┄┄┄┄┄┄┄┄┄┄6分
(Ⅱ) 对
对 的回归直线方程为
的回归直线方程为
 .
.
当 时,
时, ,
, .
.
当 时,
时, ,
, .
.
所以 岁和
岁和 岁的残差分别为
岁的残差分别为 和
和 .
.
┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄12分
证明:由于 ,
, ,
,
所以只需证明 .
.
展开得 ,即
,即 .
.
所以只需证 .
.
因为 显然成立,
显然成立,
所以 .┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄12分
.┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄12分
18B. (本小题满分12分)
证明:(Ⅰ)因为 ,所以
,所以 .
.
由于函数 是
是 上的增函数,
上的增函数,
所以 .
.
同理,  .
.
两式相加,得 .┄┄┄┄┄┄┄┄┄┄┄┄6分
.┄┄┄┄┄┄┄┄┄┄┄┄6分
(Ⅱ)逆命题:
若 ,则
,则 .
.
用反证法证明
假设 ,那么
,那么

所以 .
.
这与 矛盾.故只有
矛盾.故只有 ,逆命题得证.
,逆命题得证.
┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄12分
解:(Ⅰ)由于 ,且
,且 .
.
所以当 时,得
时,得 ,故
,故 .
.
从而 .┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄6分
.┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄6分
(Ⅱ)数列 不可能为等差数列,证明如下:
不可能为等差数列,证明如下:
由 ,
, 得
得
若存在 ,使
,使 为等差数列,则
为等差数列,则 ,
,
即 ,解得
,解得 .
.
于是 ,
, .
.
这与 为等差数列矛盾.所以,对任意
为等差数列矛盾.所以,对任意 ,数列
,数列 都不可能是等差数列.
都不可能是等差数列.
┄┄┄┄┄┄┄┄┄┄┄┄12分
19B. (本小题满分12分)
解:(Ⅰ) ,
, .
.
 ,
, .┄┄┄┄┄┄┄┄┄┄┄6分
.┄┄┄┄┄┄┄┄┄┄┄6分
(Ⅱ)由(Ⅰ)可得 ,
,
 ,
,
 .
.
猜想: 是公比为
是公比为 的等比数列.
的等比数列.
证明如下:因为
 ,
,
又 ,所以
,所以 ,
,
所以数列 是首项为
是首项为 ,公比为
,公比为 的等比数列.┄┄┄┄┄┄┄┄┄┄┄┄12分
的等比数列.┄┄┄┄┄┄┄┄┄┄┄┄12分
 ,
, ,
,