题号
一
二
三
成绩
17
18
19
20
21
22
分数
 第三章 数列测试卷
第三章 数列测试卷
一. 选择题(每题仅有一个答案正确,每小题5分,共60分,把答案写在下面的方框内)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
1.某数列既是等差数列,又是等比数列,则这个数列为
A.常数列 B.公差为零的等差数列 C.公比为1的等比数列 D.这样的数列不存在
2.a,b,c∈R,则“b2=ac且b≠
A.充分不必要 B.必要而不充分 C.充要 D.既不充分也不必要
3.已知数列 ,…,则
,…,则 是该数列的第( )项.
是该数列的第( )项.
A.5 B.6 C.7 D.8
4.设Sn等差数列 的前n项和,若
的前n项和,若 等于
等于
A.6 B. C.12 D.
C.12 D.
5.等差数列
A.48 B.49 C.50 D.51
6.等差数列{an}的前m项和是30,前2m项和是100,则它的前3m项和是
A.130 B.170 C.210 D.260
7.在等差数列{an}中,公差 的值为
的值为
A. B.
B. C.
C. D.1
D.1
8.在正项等比数列 中,
中, ,那么数列
,那么数列 的通项公式为
的通项公式为
A. B.
B. C.
C. D.
D.
9.等比数列{an}中,S2=7,S6=91,则S4是
A.28 B.32 C.35 D.49
10.等比数列 中,
中,  则
则 的前4项和为
的前4项和为
A. 81 B .120 C. 168 D .192
11.若Sn是数列{an}的前n项和,且 则
则 是
是
A.等比数列,但不是等差数列 B.等差数列,但不是等比数列
C.等差数列,而且也是等比数列 D.既非等比数列又非等差数列
12.数列{an}的通项公式an= ,则其前n项和Sn=
,则其前n项和Sn=
A. B.
B. C.
C. D.
D.
二.填空题(每小题4分,共16分)
13.若数列{an}为等比数列,则下面四个命题:①数列{an3}也是等比数列;②数列{-an}也是等比数列;③数列{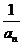 }也是等比数列;④数列{
}也是等比数列;④数列{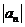 }也是等比数列,其中正确的命题是_____________________
}也是等比数列,其中正确的命题是_____________________
14.若数列{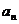 }满足
}满足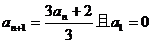 ,则
,则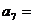 _______________________
_______________________
15.设a=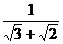 ,b=
,b=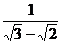 ,则a、b的等差中项为________________________
,则a、b的等差中项为________________________
16.在等比数列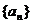 中,若
中,若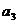 ,
,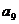 是一元二次方程
是一元二次方程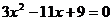 的两根,则
的两根,则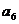 =_____________
=_____________
三.解答题(共6题,共74分)
17.(12分)在等比数列{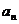 }中,已知
}中,已知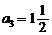 ,
,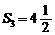 ,求
,求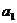 与q.
与q.
18.(12分)求数列 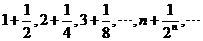 的前n项和
的前n项和
 19.(12分)在各项均为正数的等比数列{an}中, 若a5a6=9,
19.(12分)在各项均为正数的等比数列{an}中, 若a5a6=9,
求log3a1+log3a2+…+log3a10的值
20.(12分)三个数成等比数列,若第二个数加4 就成等差数列,再把第三个数加32又成等比数列,求这三个数.
21.(12分)用分期付款方式购买P4型家用电脑,价格为每台11500元,可用以下方式付款,购买当于先付1500元,以后每月交付500元,并先加付欠款利息,月利率为1%(即欠款的1%,利息不计入欠款),在交付1500元后的第一个月为分期付款的第一个月,问分期付款的第10个月交付多少钱?全部贷款付清后,买这台电脑实际花了多少钱?
22.(14分)设各项均为正数的数列{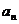 }的前n项和为Sn,且满足:
}的前n项和为Sn,且满足: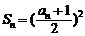 .
.
(1)求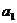 ,
,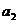 ,
,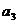 ;
;
(2)求出数列{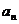 }的通项公式(写出推导过程);
}的通项公式(写出推导过程);
(3)设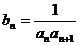 ,求数列{
,求数列{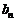 }的前n项和
}的前n项和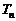 .
.
第三章 数列测试卷答案
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
C
B
A
C
C
A
D
A
B
B
A
13
①②③④
14
4
15
二.填空题(每小题4分,共16分)
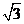
16
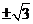
三.解答题(共6题,共74分)
17.(12分)解:当q=1时,a1=a3=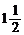 ,这时S3=3a1=
,这时S3=3a1=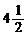 ,满足条件.
,满足条件.
当q≠1时,由已知得: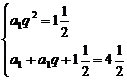 解得:
解得: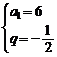
∴所求为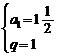 或
或 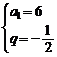 .
.
18.(12分)解: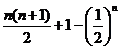
19.(12分)解:10
20.(12分)解:设这三个数为:a,aq,aq2,则
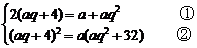
由②得: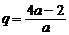 ③,代入①并整理得:9a2-20a+4=0
③,代入①并整理得:9a2-20a+4=0
解得a=2或a=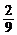
当a=2时,由③得q=3,当a=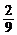 时,由③得q=-5
时,由③得q=-5
∴所求的三个数为:2,6,18 或 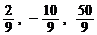 .
.
21.(12分)解:每月付500元,所欠10000元需20个月付清
第一个月付:a1=500+10000×1%=500+100=600?5(1?1)
第二个月付:a2=500+(10000-500)×1%=595=500+100?5=600?5(2?1)
第三个月付:an=500+[10000?500(n?1)]×1%=600?5(n?1)=605?5n(1≤n≤20)
当n=10时,a10=600?5(10?1)=555
∵an?an―1=(605?5n)?[605?5(n?1)=?5=d
∴S20=600×20+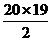 (-5)=11500
11050+1500=12550
(-5)=11500
11050+1500=12550
因此第10个月应付555元,买这电脑实际花了12550元。
22.(14分)解:(1) 由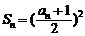 得:
得: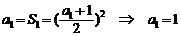
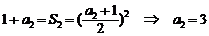 ,
,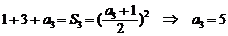
(2) 当n≥2时,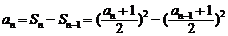
整理得:(an-1)2=(an-1+1)2 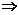 an-an-1=2
an-an-1=2
∴{an}是公差为2的等差数列,∴an=a1+(n-1)×2,an=2n-1.
(3) 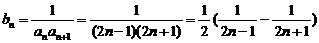
∴