山东省兖州高补学校2009届高三模拟
2009年高补学校
数学试卷(理科)
本试卷分第Ⅰ卷(选择题)和第Ⅱ第(选择题)两部分,共1 50分,考试时间1 20分钟
第Ⅰ卷
选择题(本题共12个小题,每小题 5分,共60分.在每小题给出的四个选项中,有1个是正确的)
1.含有3个元素的集合既可表示为 ,又可表示为
,又可表示为 ,则
,则
 的值是( )
的值是( )
A.1 B. C.
C. D.
D.
2.复数 是纯虚数,则
是纯虚数,则 ( )
( )
A. B.
B. D.
D.
3.给出如下三个命题:
①若“P且q”为假命题,则p、q均为假命题;
②命题“若 且
且 ,则
,则 ”的否命题为“若
”的否命题为“若 且
且 ,则
,则 ”;
”;
③四个实数a、b、c、d依次成等比数列的必要而不充分条件是ad=bc;
④ 在 中,“
中,“ ”是“
”是“ ”的充分不必要条件。
”的充分不必要条件。
其中不正确的合题的个数是 ( )
A.4
B.
4.在棱长为2的正方体 中,
中,  是
是 的中点,则
的中点,则 到平面
到平面 的距离是( )
的距离是( )
A.  B.
B. C.
C. D.
D.
5.已知函数 则二项式
则二项式 展开式中数项是( )
展开式中数项是( )
A.第7项 B.第8项 C.第9项 D.第10项
6.若 ,则
,则 大小关系是( )
大小关系是( )
A. B.
B. C.
C. D.
D.
7.等差数列 的前
的前 项和为
项和为 ,若
,若 …
… 则
则 等于( )
等于( )
A. B.
B. C.0 D.1
C.0 D.1
8.在如图所示的流程图中,若输入值分别为 则输出的
则输出的
数为( )
 |
A.
 B.
B.  C.
C. D.不确定
D.不确定
 |
9.如图,样本数为9的四组数据,它们的平均数都是5,频率条形图如下,则标准差最大的一组是 ( )
10.曲线 和直线
和直线 在
在 轴右侧的交点按横坐标从小到大依次记为
轴右侧的交点按横坐标从小到大依次记为 …则
…则 等于
等于
A. B.
B. C.
C. D.
D.
11.已知抛物线 与双曲线
与双曲线 有相的焦点
有相的焦点 ,点
,点 是两曲线的一个交点,且
是两曲线的一个交点,且 轴,若
轴,若 为双曲线的一条渐近线,则
为双曲线的一条渐近线,则 的倾斜角所在的区间可能是 ( )
的倾斜角所在的区间可能是 ( )
A. B.
B.  C.
C. D.
D.
12.设函数 在定义域为
在定义域为 ,如果对任意的
,如果对任意的 ,存在唯一的
,存在唯一的 ,便
,便 (
( 为常数)成立,则称函数
为常数)成立,则称函数 在
在 上的均值为
上的均值为 ,给出下列四个函数:①
,给出下列四个函数:① ;②
;② ③
③ ;④
;④ ,则满足在其定义域上的均值为2的所有函数是 ( )
,则满足在其定义域上的均值为2的所有函数是 ( )
A. ①② B. ③④ C.②④ D.①③
第Ⅱ卷(非选择题,共90分)
注意事项:1.第Ⅱ卷共6页,用蓝、黑色的钢笔或圆珠笔直接答在答题纸上。
2.答卷前,请将密封线内的项目填写清楚。
二.填空题:本大题共6小题,每小题4分,共24分,把答案填在答题纸上相应的横线上。
13.观察下列式子: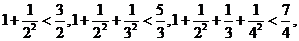 ……,则可以猜想:当
……,则可以猜想:当 时,有___________________。
时,有___________________。
14.已知二项式 的展开式中
的展开式中 项的系数与
项的系数与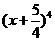 的展开式中
的展开式中 项的系数相等,则
项的系数相等,则 _________。
_________。
15.在三棱锥 中,侧棱
中,侧棱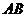 、
、 、
、 两两垂直,
两两垂直, 、
、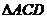 、
、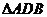 的面积分别为
的面积分别为 、
、 、
、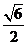 ,则三棱锥
,则三棱锥 的外接球的体积为_____________。
的外接球的体积为_____________。
16.某同学在研究函数 时,分别给出下面几个结论:
时,分别给出下面几个结论:
①等式 在
在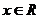 时恒成立; ②函数
时恒成立; ②函数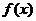 的值域为
的值域为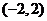
③若 则一定有
则一定有 ; ④函数
; ④函数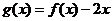 在
在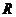 上有三个零点。
上有三个零点。
其中正确结论的序号有_______________(请将你认为正确的结论的序号都填上)
三.解答题:本大题6小题,共74分,解答应写出文字说明,证明过程或演算步骤。
17.(本小题满分12分)
 中,角
中,角 、
、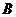 、
、 所对的边分别为
所对的边分别为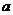 、
、 、
、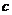 且
且
(1)求角的 大小;
大小;
(2)若向量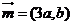 ,向量
,向量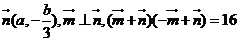 ,求
,求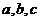 的值。
的值。
18.(本小题满分12分)
有编号为1,2,3,…, 的
的 个学生,入坐编号为1,2,3,…
个学生,入坐编号为1,2,3,… 的
的 个座位,每个学生规定坐一个座位,设学生所坐的座位号与该生的编号不同的学生人数为
个座位,每个学生规定坐一个座位,设学生所坐的座位号与该生的编号不同的学生人数为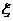 ,已知
,已知 时,共有6种坐法。
时,共有6种坐法。
(Ⅰ)求 的值;
的值;
 (Ⅱ)求随机变量
(Ⅱ)求随机变量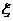 的概率分布列和数学期望。
的概率分布列和数学期望。
19.(本小题满分12分)
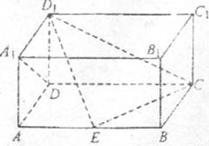
如图,在长方体
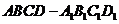 中
中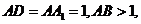 点
点
 在棱
在棱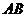 上移动,小蚂蚁从点
上移动,小蚂蚁从点 沿长方体的表
沿长方体的表
面爬到点 ,所爬的最短路程为
,所爬的最短路程为 。
。
(1)求证:
(2)求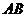 的长度:
的长度:
(3)在线段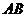 上是否存在点
上是否存在点 ,使得三面角
,使得三面角 的大小为
的大小为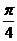 。若存在,确定点
。若存在,确定点 的位置;若不存在,请说明理由。
的位置;若不存在,请说明理由。
20.(本小题满分12分)
数列 的各项均为正数,前
的各项均为正数,前 项和为
项和为 ,对于
,对于 ,总有
,总有 成等比数列,且
成等比数列,且
(1)求数列 的通项公式:
的通项公式:
(2)对任意给定的正整数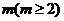 ,作数列
,作数列 ,使
,使 ,且
,且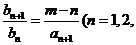 …,
…, 求
求 …
…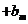 的值;
的值;
21.(本小题满分12分)
已知椭圆 的上、下焦点分别为
的上、下焦点分别为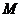 、
、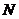 ,点
,点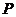 为坐标平面内的动点,满足
为坐标平面内的动点,满足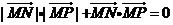
(1)求动点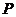 的轨迹
的轨迹 的方程:
的方程:
(2)过点 作曲线
作曲线 的两条切线,切点分别为
的两条切线,切点分别为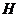 、
、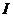 ,求直线
,求直线 的方程:
的方程:
(3)在直线 上否存在点
上否存在点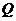 ,过该点作曲线
,过该点作曲线 的两条切线,切点分别为
的两条切线,切点分别为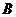 、
、 ,使得
,使得 ,若存,求出该点的坐标;若不存在,试说明理由。
,若存,求出该点的坐标;若不存在,试说明理由。
22.(本小题满分11分)
已知函数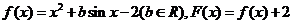 ,且对于任意实数
,且对于任意实数 ,恒有
,恒有
(1)求函数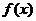 的解析式;
的解析式;
(2)已知函数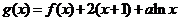 在区间
在区间 上单调,求实数
上单调,求实数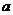 的取值范围;
的取值范围;
(3)函数 有几个零点?
有几个零点?
数学试卷(理科)
1―5:B D B B C 6―10:D C A D A 11―12:D D
二.填空题:
13. 14.
14.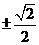 15.
15. 16.①②③
16.①②③
三.解答题:
17.解:(1)∵
∴ ………………………………2分
………………………………2分
∴ ,∴
,∴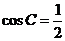 或
或
∵ ,∴
,∴ ………………………………………………………………4分
………………………………………………………………4分
(2)∵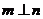 ∴
∴ ,即
,即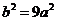
又 ∴
∴ ,即
,即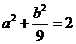 ②…………6分
②…………6分
由①②可得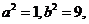 ∴
∴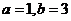 ……………………………………………8分
……………………………………………8分
又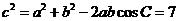 ,∴
,∴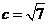 …………………………………………12分
…………………………………………12分
18.解:(Ⅰ)∵当 时,有
时,有 种坐法 ………………………………………………2分
种坐法 ………………………………………………2分
∴ ,即
,即
 或
或 (舍去) ∴
(舍去) ∴ …………………………………4分
…………………………………4分
(Ⅱ)∵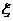 的可能取值是0,2,3,4,
的可能取值是0,2,3,4,
又∵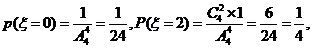
 ……………………………………8分
……………………………………8分
∴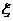 的概率分布为:
的概率分布为:
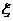
0
2
3
4
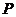
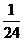


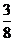
……………10分
则 。 …………………………………12分
。 …………………………………12分
 19.解:(1)证明:连结
19.解:(1)证明:连结 ,由长方体的性质可知:
,由长方体的性质可知: 平面
平面 ,∴
,∴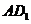 是
是 在平面
在平面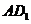 内的射影。又∵
内的射影。又∵
∴
∴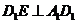 (三垂线定理)………………4分
(三垂线定理)………………4分
(2)设 ,∵四边形
,∵四边形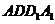 是正方形,
是正方形,
∴小蚂蚁从点 沿长方体的表面爬到点
沿长方体的表面爬到点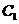 可能
可能
有两种途径,如图甲的最短路程为

如图乙的最短路?为
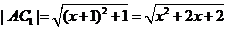
∵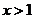
∴
∴ ∴
∴ …………9分
…………9分
(3)假设存在,平面 的法向量
的法向量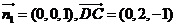
设平面 的法向量
的法向量 则
则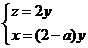
∴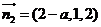 ………………………………………………………………………10分
………………………………………………………………………10分
由题意得:
解得: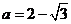 或
或 (舍去)
(舍去)
即当点 离
离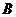 为
为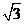 时,三面角
时,三面角 的大小为
的大小为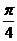 。 …………………12分
。 …………………12分
20.解:(1)由 知,
知,
所以 又
又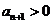 ,所以
,所以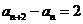 ,
,
若 为奇数,由
为奇数,由 得
得 。
。
若 为偶数,则由
为偶数,则由 得
得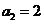 ,所以
,所以 。
。
综上所述, ………………………………………………………4分
………………………………………………………4分
(2)由于 ……,
……, ,
,
将以上各式左右两边分别对应相乘得到:
(2)设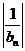 的前
的前 项和为
项和为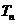 ,当
,当 时,
时, ∴
∴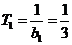 ;(8分)
;(8分)
 时,
时,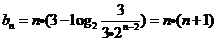 ,∴
,∴ (10分)
(10分)
∴
∴ (12分)
(12分)
21.解:(1)由题意知 ,设
,设 。由余弦定理得
。由余弦定理得
 (2分)
(2分)
又 (4分)
(4分)
当且仅当 时,
时,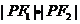 取最大值,此时
取最大值,此时 取最小值
取最小值
令 ,∵
,∵ ,∴
,∴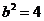 。
。
故所求点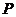 的轨迹方程为
的轨迹方程为 (6分)
(6分)
(2)设 则由
则由 可得
可得 ,
,
故 (8分)
(8分)
∵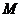 、
、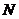 在动点
在动点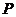 的轨迹上,故
的轨迹上,故 且
且 消去
消去 得
得
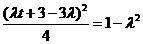 ,解得
,解得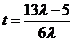 ,又
,又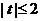 ,
,
∴ ,得解
,得解 。故
。故 的取值范围是
的取值范围是 。
(12分)
。
(12分)
22.解:(Ⅰ) ,令
,令 ,得
,得 或
或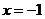 。 (2分)
。 (2分)
当 时,
时, 在
在 上单调递增;
上单调递增;
当 时,
时, 在
在 上单调递减,
上单调递减,
而 ,∴当
,∴当 时,
时,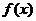 的值域是
的值域是 。 (4分)
。 (4分)
(Ⅱ)设函数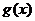 在
在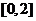 上的值域是A,
上的值域是A,
∵若对任意 ,总存在
,总存在 ,使
,使 ,∴
,∴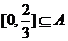 (6分)
(6分)
 .
.
①当 时,
时, ,
,
∴函数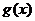 在
在 上单调递减,
上单调递减,
∵ ∴当
∴当 时,不满足
时,不满足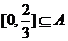 ; (8分)
; (8分)
②当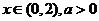 时,
时, ,
,
令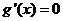 ,得
,得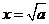 或
或 (舍去)。
(9分)
(舍去)。
(9分)
(Ⅰ)当 时,
时, 的变化如下表:
的变化如下表:

0



2
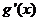
-
0
+
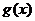
0
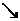
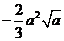


∴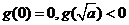 , ∵
, ∵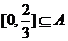 ,
,
∴ ,解得
,解得 。
(11分)
。
(11分)
(Ⅱ)当 时,
时,
∴函数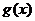 在(0,2)上单调递减,
在(0,2)上单调递减,
∵
∴当 时,不满足
时,不满足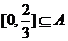 .
(13分)
.
(13分)
综上可知,实数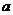 的取值 范围是
的取值 范围是 .
(14分)
.
(14分)