2003年全国普通高等学校招生全国统一考试(上海卷)
物理
第Ⅰ卷
一、(40分)选择题,本大题共8小题,每小题5分,每小题给出的四个答案中,至少有一个是正确的。把正确答案全选出来,并将正确答案前面的字母填写在题后的方括号内。每一小题全选对的得5分,选对但不全,得部分分;有选错或不答的,得0分。填写在方括号外的字母,不作为选出的答案。
1.在核反应方程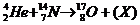 的括弧中,X所代表的粒子
的括弧中,X所代表的粒子
A.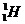 B.
B.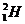 C.
C.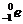 D.
D.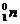
2.关于机械波,下列说法正确的是
A.在传播过程中能传递能量 B.频率由波源决定
C.能产生干涉,衍射现象 D.能在真空中传播
3.爱因斯坦由光电效应的实验规律,猜测光具有粒子性,从而提出光子说,从科学研究的方法来说,这属于
A.等效替代 B.控制变量 C.科学假说 D.数学归纳
4.一个质量为0.3kg的弹性小球,在光滑水平面上以6m/s的速度垂直撞到墙上,碰撞后小球沿相反方向运动,反弹后的速度大小与碰撞前相同,则碰撞前后小球速度变化量的大小△v和碰撞过程中墙对小球做功的大小W为
A.△v=0 B.△v=12m/s C.W=0 D.W=10.8J
5.一负电荷仅受电场力的作用,从电场中的A点运动到B点,在此过程中该电荷作初速度为零的匀加速直线运动,则A、B两点电场强度EA、EB及该电荷的A、B两点的电势能εA、、εB之间的关系为
A.EA=EB. B.EA<EB. C.εA=εB. D.εA>εB
6.粗细均习的电阻丝围成的正方形线框置于有界匀强磁场中,磁场方向垂直于线框平面,其边界与正方形线框的边平行。现使线框以同样大小的速度沿四个不同方向平移出磁场,如图所示,则在移出过程中线框的一边a、b两点间电势差绝对值最大的是
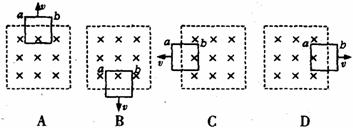
7.一质量不计的直角形支架两端分别连接质量为m和2m的小球A和B。支架的两直角边长度分别为2l和l,支架可绕固定轴O在竖直平面内无摩擦转动,如图所示。开始时OA边处于水平位置,由静止释放,则
A.A球的最大速度为2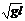
B.A球速度最大时,两小球的总重力势能最小
C.A球速度最大时,两直角边与竖直方向的夹角为45°
D.A、B两球的最大速度之比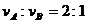
8.劈尖干涉是一种薄膜干涉,其装置如图1所示,将一块平板玻璃放置在另一平板玻璃之上,在一端夹入两张纸片,从而在两玻璃表面之间形成一个劈形空气薄膜。当光垂直入射后,从上往下看到的干涉条纹如图2所示。干涉条纹有如下特点:
(1)任意一条明条纹或暗条纹所在位置下面的薄膜厚度相等;
(2)任意相邻明条纹和暗条纹所对应的薄膜厚度差恒定。现若在图1装置中抽去一张纸片,则当光垂直入射到新的劈形空气薄膜后,从上往下观察到的干涉条纹
A.变疏 B.变密 C.不变 D.消失
第二卷
二、(20分)填空题,本大题共5小题,每小题4分。答案写在题中横线上的空白处或指定位置,不要求写出演算过程。
9.卢瑟福通过 实验,发现了原子中间有一个很小的核,并由此提出了原子的核式结构模型。右面平面示意图中的四条线表示α粒子运动的可能轨迹,在图中完成中间两条α粒子的运动轨迹。

10.细绳的一端在外力作用下从t=0时刻开始做简谐振动,激发出一列简谐横波。在细绳上选取15个点,图1为t=0时刻各点所处的位置,图2为t=T/4时刻的波形图(T为波的周期)。在图3中画出t=3T/4时刻的波形图。

11.有质量的物体周围存在着引力场。万在引力和库仑力有类似的规律,因此我们可以用定义静电场场强的方法来定义引力场的场强。由此可得,与质量为M的质点相距r处的引力场场强的表达式为EG= (万有引力恒量用G表示)。
12.若氢原子的核外电子绕核作半径为r的匀速圆周运动,则其角速度ω= ;
电子绕核的运动可等效为环形电流,则电子运动的等效电流I= 。(已知电子的质量为m,电量为e,静电力恒量用k表示)
13.某登山爱好者在攀登珠穆朗峰的过程中,发现他携带的手表表面玻璃发生了爆裂。这种手表是密封的,出厂时给出的参数为:27℃时表内气体压强为1×105Pa;在内外压强差超过6×104Pa时,手表表面玻璃可能爆裂。已知当时手表处的气温为-13℃,则手表表面玻璃爆裂时表内气体压强的大小为 Pa;已知外界大气压强随高度变化而变化,高度每上升12m,大气压强降低133Pa,设海平面大气压为1×105Pa,则登山运动员此时的海拔高度约为 m。
三、(30分)实验题。其中第14、15小题和第17小题(1)为选择题,选出全部正确答案,选对但不全,得部分分;有选错或不答的,得0分。
14.(5分)如图所示,在研究平抛运动时,小球A沿轨道滑下,离开轨道末端(末端水平)时撞开轻质接触式开关S,被电磁铁吸住的小球B同时自由下落。改变整个装置的高度H做同样的实验,发现位于同一高度的A、B两球总是同时落地,该实验现象说明了A球在离开轨道后
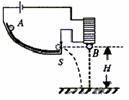
A.水平方向的分运动是匀速直线运动。
B.水平方向的分运动是匀加速直线运动。
C.竖直方向的分运动是自由落体运动。
D.竖直方向的分运动是匀速直线运动。
15.(5分)在右图所求的光电管的实验中,发现用一定频率的A单色照射光电管时,电流表指针会发生偏转,而用另一频率的B单色光照射时不发生光电效应,那么
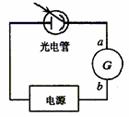
A.A光的频率大于B光的频率。
B.B光的频率大于A光的频率。
C.用A光照射光电管时流过电流表G的电流方向是a流向b。
D.用A光照射光电管时流过电流表G的电流方向是b流向a。
16.(6分)如图所示,在“有固定转动轴物体的平衡条件实验中,调节力矩盘使其平衡,弹簧秤的读数为 N,此时力矩盘除受到钩码作用力F1、F2、F3和弹簧拉力F4外,主要还受力和 力的作用,如果每个钩码的质量均为0.1kg,盘上各圆的半径分别是0.05m、0.10m、0.15m、0.20m(取g=10m/s2),则F2的力矩是 N?m。有同学在做这个实验时,发现顺时针力矩之和与逆时针力矩之和存在较大差距。检查发现读数和计算均无差错,请指出造成这种差距的一个可能原因,并提出简单的检验方法(如例所示,将答案填在下表空格中)。
可能原因
检验方法
例
力矩盘面没有调到竖直
用一根细线挂一钩码靠近力矩盘面,如果细线与力矩盘面间存在一个小的夹角,说明力矩盘不竖直。
答
17.(7分)有同学在做“研究温度不变时气体的压强跟体积的关系”实验时,用连接计算机的压强传感器直接测得注射器内气体的压强值。缓慢推动活塞,使注射器内空气柱从初始体积20.0ml变为12.0ml。实验共测了5次,每次体积值直接从注射器的刻度上读出并输入计算机,同时由压强传感器测得对应体积的压强值。实验完成后,计算机屏幕上立刻显示出如下表中所示的实验结果。

序号
V (ml)
P (×105Pa)
PV (×105Pa?ml)
1
20.0
1.0010
20.020
2
18.0
1.0952
19.714
3
16.0
1.2313
19.701
4
14.0
1.4030
19.642
5
12.0
1.6351
19.621
(1)仔细观察不难发现,pV(×105Pa?ml)一栏中的数值越来越小,造成这一现象的可能原因是
A.实验时注射器活塞与筒壁间的摩擦力不断增大。
B.实验时环境温度增大了。
C.实验时外界大气压强发生了变化。
D.实验时注射器内的空气向外发生了泄漏。
(2)根据你在(1)中的选择,说明为了减小误差,应采取的措施是:
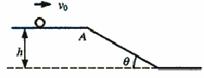
18.(7分)图1为某一热敏电阻(电阻值随温度的改变而改变,且对温度很敏感)的I-U关系曲线图。
(1) 为了通过测量得到图1所示I-U关系的完整曲线,在图2图3两个电路中应选择的是图 ;简要说明理由:
(电源电动势为9V,内阻不计,滑线变阻器的阻值为0-100Ω)。
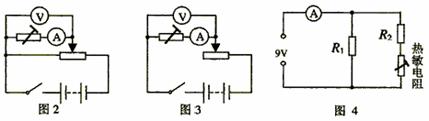
(2)在图4电路中,电源电压恒为9V,电流表读数为70mA,定值电阻R1=250Ω。由热敏电阻的I-U关系曲线可知,热敏电阻两端的电压为 V;电阻R2的阻值为 Ω。
(3)举出一个可以应用热敏电阻的例子:
。
四、(60分)计算题。
19.(10分)如图所示,1、2、3为p-V图中一定量理想气体的三个状态,该理想气体由状态1经过程1-3-2到达状态2。试利用气体实验定律证明: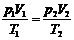
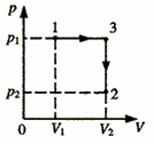
20.(10分)如图所示,一高度为h=0.2m的水平面在A点处与一 倾角为θ=30°的斜面连接,一小球以v0=5m/s的速度在平面上向右运动。求小球从A点运动到地面所需的时间(平面与斜面均光滑,取g=10m/s2)。
某同学对此题的解法为:小球沿斜面运动,
则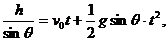 由此可求得落地的时间t。
由此可求得落地的时间t。
问:你同意上述解法吗?若同意,求出所需的时间;若不同意,则说明理由并求出你认为正确的结果。
21.(12分)质量为m的飞机以水平速度v0飞离跑道后逐渐上升,若飞机在此过程中水平速度保持不变,同时受到重力和竖直向上的恒定升力(该升力由其它力的合力提供,不含重力)。今测得当飞机在水平方向的位移为l时,它的上升高度为h,
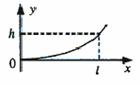
求:(1)飞机受到的升力大小;
(2)从起飞到上升至h高度的过程中升力所作的功及在高度h处飞机的动能。
22.(14分)如图所示,OACO为置于水平面内的光滑闭合金属导轨,O、C处分别接有短电阻丝(图中粗线表法),R1=4Ω、R2=8Ω(导轨其它部分电阻不计)。导轨OAC的形状满足方程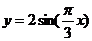 (单位:m)。磁感强度B=0.2T的匀强磁场方向垂直于导轨平面。一足够长的金属棒在水平外力F作用下,以恒定的速率v=5.0m/s水平向右在导轨上从O点滑动到C点,棒与导思接触良好且始终保持与OC导轨垂直,不计棒的电阻。
(单位:m)。磁感强度B=0.2T的匀强磁场方向垂直于导轨平面。一足够长的金属棒在水平外力F作用下,以恒定的速率v=5.0m/s水平向右在导轨上从O点滑动到C点,棒与导思接触良好且始终保持与OC导轨垂直,不计棒的电阻。
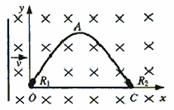
求:(1)外力F的最大值;
(2)属棒在导轨上运动时电阻丝R1上消耗的最大功率;
(3)在滑动过程中通过金属棒的电流I与时间t的关系。
23.(14分)为研究静电除尘,有人设计了一个盒状容器,容器侧面是绝缘的透明有机玻璃,它的上下底面是面积A=0.04m2的金属板,间距L=0.05m,当连接到U=2500V的高压电源正负两极时,能在两金属板间产生一个匀强电场,如图所示,现把一定量均匀分布的烟尘颗粒密闭在容器内,每立方米有烟尘颗粒1013个,假设
这些颗粒都处于静止状态,每个颗粒带电量为q=+1.0×10-17C,质量为m=2.0×10-15kg,不考虑烟尘颗粒之间的相互作用和空气阻力,并忽略烟尘颗粒所受重力。
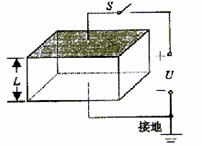
求合上电键后:
(1)经过多长时间烟尘颗粒可以被全部吸附?
(2)除尘过程中电场对烟尘颗粒共做了多少功?
(3)经过多长时间容器中烟尘颗粒的总动能达到最大?