山东省曲阜师大附中2009届高三高考模拟
理科数学
本试卷分第I卷(选择题)和第Ⅱ卷(非选择)两部分,第I卷1至2页,第Ⅱ卷3至4页。满分150分。考试用时120分钟。考试结束后,将本试卷和答题卡一并交回。
第I卷(共60分)
注意事项:
1.答第I卷前,考生务必用0.5毫米黑色签字笔将姓名、座号、准考证号填写在答题卡和试卷规定的位置。
2.第I卷共2页。答题时,考生须用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案。在试卷上作答无效。
参考公式:
球的体积公式: ,其中
,其中 是球的半径。
是球的半径。
锥体的体积公式: ,其中S是锥体的底面积。h是锥体的高。
,其中S是锥体的底面积。h是锥体的高。
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.若将复数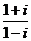 表示为
表示为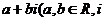 是虚数单位)的形式,则
是虚数单位)的形式,则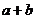 等于
等于
A.0
B.
2.已知集合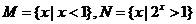 ,则
,则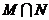 等于
等于
A.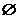 B.
B.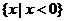 C.
C.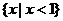 D.
D.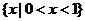
 3.设
3.设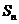 是等差数列
是等差数列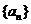 的前
的前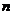 项和,若
项和,若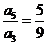 ,则
,则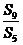 =
=
A.1
B.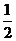
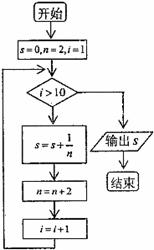
4.如图,程序框图所进行的求和运算是
A.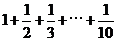 B.
B.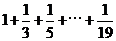
C.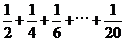 D.
D.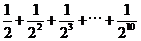
5.下图是某学校举行的运动会上,七位评委为某体操项目
打出的分数的茎叶统计图,去掉一个最高分和一个最低
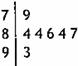 分后,所剩数据的平均数的方差分别为
分后,所剩数据的平均数的方差分别为
A.84,4.84 B.84,1.6
C.85,1.6 D.85,4
 6.函数
6.函数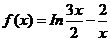 的零点一定位于区间
的零点一定位于区间
A.(1,2) B.(2,3) C.(3,4) D.(4,5)
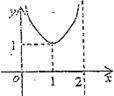
7.函数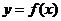 的图象如右图所示,
的图象如右图所示,
则函数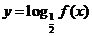 的图像大致是
的图像大致是
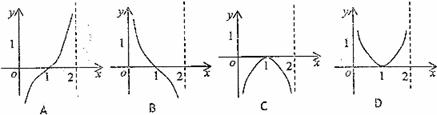
8.已知函数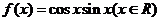 ,给出下列四个命题:
,给出下列四个命题:
①若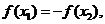 则
则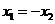 ; ②
; ②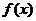 的最小正周期是2
的最小正周期是2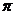 ;
;
③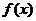 在区间
在区间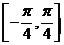 上是增函数; ④
上是增函数; ④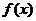 的图象关于直线
的图象关于直线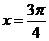
其中真命题是
A.①②④ B.①③ C.②③ D.③④
9.若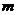 、
、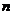 是两条不同的直线,
是两条不同的直线,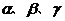 是三个不同的平面,则下列命题中为真命题的是
是三个不同的平面,则下列命题中为真命题的是
A.若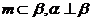 ,则
,则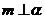 B.若
B.若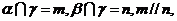 则
则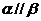
C.若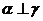 ,
,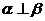 ,则
,则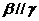 D.若
D.若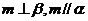 ,则
,则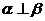
10.在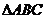 中,已知
中,已知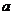 、
、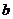 、
、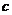 成等比数列,且
成等比数列,且 ,则
,则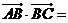
A.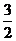 B.
B.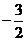 C.3
D.-3
C.3
D.-3
11.已知圆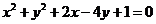 关于直线
关于直线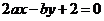
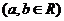 对称,则
对称,则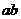 的取值范围是
的取值范围是
A.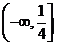 B.
B.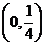 C.
C.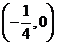 D.
D.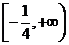
12.若函数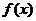 为奇函数,且在
为奇函数,且在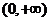 内是增函数,又
内是增函数,又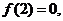 则
则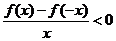 的解集为
的解集为
A.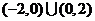 B.
B.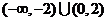
C.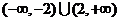 D.
D.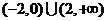
第Ⅱ卷(共90分)
注意事项:
第Ⅱ卷共2页。考生必须使用0.5毫米黑色签字笔在答题卡上题目的指定答题区域内作
答,填空题请直接写答案,解答题应写出文字、证明过程或演算步骤。在试卷上作答无效。
二、填空题:本大题共4小题,每小题4分,共16分。
13.抛物线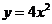 的焦点坐标是__________。
的焦点坐标是__________。
14.已知正方体外接球的体积是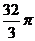 ,则正方体的棱长等于__________。
,则正方体的棱长等于__________。
15.已知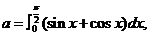 则二项式
则二项式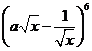 展开式中含
展开式中含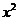 项的系数是_____。
项的系数是_____。
16.设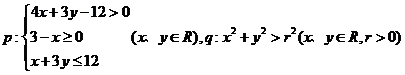 ,若
,若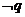 是
是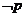 的充分不必要条件,则
的充分不必要条件,则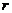 的取值范围是__________。
的取值范围是__________。
三、解答题:本大题共6小题,共74分。
17.(本小题满分12分)
已知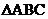 中,角A、B、C的对边分别为
中,角A、B、C的对边分别为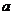 、
、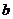 、
、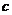 ,且满足
,且满足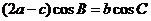 。
。
(1)求角B大小;
(2)设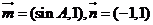 ,求
,求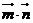 的最小值。
的最小值。
18.(本小题满分12分)
已知数列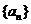 的各项均为正数,
的各项均为正数,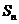 为其前
为其前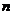 项和,对于任意的
项和,对于任意的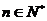 满足关系式
满足关系式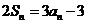 。
。
(1)求数列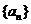 的通项公式;
的通项公式;
(2)设数列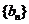 的通项公式是
的通项公式是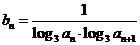 ,前
,前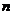 项和为
项和为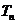 ,
,
求证:对于任意的正数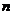 ,总以后
,总以后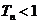 。
。
19.(本小题满分12分)
某出版社准备举行一次高中数学新教材研讨会,会征求对新教材的使用意见,邀请50名使用不同版本教材的一线教师参加,使用不同版本教材的教师人数如下表所示:
版本
人教A版
人教B版
苏教版
北师大版
人数
20
15
10
5
(1)从这50名教师中随机选出2名教师发言,求两人所用教材版本相同的概率;
(2)若从使用人教版教材的教师中选出2名发言,设使用人教A版的教师人数为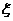 ,求
,求
随机变量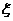 的分布列及其数学期望。
的分布列及其数学期望。
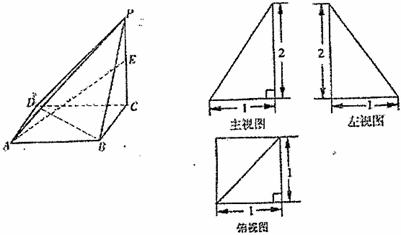
20.(本小题满分12分)
已知一四棱锥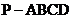 的三视图如下,E是则棱PC上的动点。
的三视图如下,E是则棱PC上的动点。
(1)求四棱锥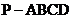 的体积;
的体积;
(2)不论点E在何位置,是否都有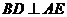 ?请证明你的结论;
?请证明你的结论;
(3)若E点为PC的中点,求二面角D-AE-B的大小。
21.(本小题满分12分)
已知椭圆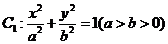 的右焦点为
的右焦点为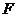 ,上顶点为
,上顶点为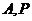 为
为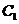 上任一点,
上任一点,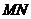 是圆
是圆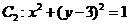 的一条直径,若与
的一条直径,若与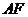 平行且在
平行且在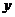 轴上的截距为
轴上的截距为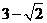 的直线
的直线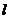 恰好与圆
恰好与圆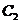 相切。
相切。
(1)求椭圆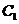 的离心率;
的离心率;
(2)若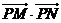 的最大值为49,求椭圆
的最大值为49,求椭圆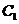 的方程。
的方程。
22.(本小题满分14分)
设函数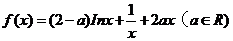
(I)当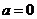 时,求
时,求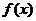 的极值;
的极值;
(Ⅱ)当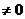 时,求
时,求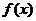 的单调区间;
的单调区间;
(Ⅲ)当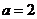 时,对于任意正整数
时,对于任意正整数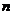 ,在区间
,在区间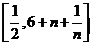 上总存在
上总存在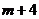 个数
个数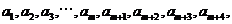 使得
使得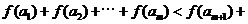
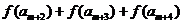 成立,试问:正整数
成立,试问:正整数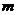 是否有最大值?若有求其最大值;否则,说明理由。
是否有最大值?若有求其最大值;否则,说明理由。
曲阜师范大学附中2009年高三模拟
一、选择题(每小题5分,共60分)
BDACC ACDDB AA
二、填空题(每小题4分,共16分)
13. ; 14.
; 14. 15.―192 16.
15.―192 16.
三、解答题(共74分)
17.解:(I)由正弦定理 ,有
,有
代入 得
得
即



(Ⅱ)
由 得
得
所以,当 时,
时, 取得最小值为0
取得最小值为0
18.解:(I)由已知得
故
即
故数列 为等比数列,且
为等比数列,且
由当 时,
时,
所以
(Ⅱ)
所以


19.解:(I)从50名教师随机选出2名的方法为 =1225,选出2人使用教材版本相同的方法数
=1225,选出2人使用教材版本相同的方法数
故2人使用版本相同的概率为 。
。
(Ⅱ)
 的分布为
的分布为

0
1
2





20.解(I)由该四棱锥的三视图可知,该四棱锥 的底面是边长为1的正方形,
的底面是边长为1的正方形,
侧棱 底面
底面 ,且
,且 ,
,
(Ⅱ)不论点E在何位置,都有
证明:连结 是正方形,
是正方形,
 底面
底面 ,且
,且 平面
平面 ,
,

又 平面
平面
 不论点
不论点 在何位置,都有
在何位置,都有 平面
平面
 不论点E在何位置,都有
不论点E在何位置,都有 。
。
(Ⅲ)以 为坐标原点,
为坐标原点, 所在的直线为
所在的直线为 轴建立空间直角坐标系如图:
轴建立空间直角坐标系如图:
则 从而
从而



设平面 和平面
和平面 的法向量分别为
的法向量分别为
 ,
,
由法向量的性质可得:

令 则
则

设二面角 的平面角为
的平面角为 ,则
,则

 二面角
二面角 的大小为
的大小为 。
。
21.解:(1)由题意可知直线 的方程为
的方程为 ,
,
因为直线与圆 相切,所以
相切,所以 ,即
,即
从而
(2)设 ,则
,则 ,
,
又
(
①当 时,
时, ,解得
,解得 ,
,
此时椭圆方程为
②当 时,
时, ,解得
,解得 ,
,
当 ,故舍去
,故舍去
综上所述,椭圆的方程为
22.解:(I)依题意,知 的定义域为(0,+
的定义域为(0,+ )
)
当 时,
时,
令 ,解得
,解得 。
。
当 时,
时, ;当
;当 时,
时,
又 所以
所以 的极小值为2-2
的极小值为2-2 ,无极大值。
,无极大值。
(Ⅱ) ;
;
令 ,解得
,解得 。
。
(1)若 令
令 ,得
,得 令
令 ,得
,得
(2)若 ,
,
①当 时,
时, ,
,
令 ,得
,得 或
或 ;
;
令 ,得
,得
②当 时,
时,
③当 时,得
时,得 ,
,
令 ,得
,得 或
或
令 ,得
,得
综上所述,当 时,
时, 的递减区间为
的递减区间为 ,递增区间为
,递增区间为
当 时,
时, 的递减区间为
的递减区间为 ;递增区间为
;递增区间为
当 时,
时, 递减区间为
递减区间为
当 时,
时, 的递减区间为
的递减区间为 ,递增区间为
,递增区间为
(Ⅲ)当 时,
时,  ,
,
由 ,知
,知 时,
时,

依题意得: 对一切正整数成立
对一切正整数成立
令 ,则
,则 (当且仅当
(当且仅当 时取等号)
时取等号)
又 在区间
在区间 单调递增,得
单调递增,得 ,
,
故 又
又 为正整数,得
为正整数,得
当 时,存在
时,存在 ,对所有
,对所有 满足条件。
满足条件。
所以,正整数 的最大值为32。
的最大值为32。