2009年广东省高中阶段学校招生模拟考试
数学试卷(六)
一、选择题(本大题共5小题,每小题3分,共15分)
1.实数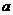 、b在数轴上的位置如图所示,则下列各式正确的是( )
、b在数轴上的位置如图所示,则下列各式正确的是( )
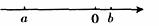
A.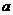 >6
>6  B.
B.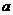 >-b C.a<b D.-
>-b C.a<b D.-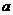 <-b
<-b
2.已知反比例函数 的图象在第二、四象限,则
的图象在第二、四象限,则 的取值范围是( )
的取值范围是( )
A.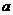 ≤2 B.
≤2 B.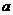 ≥
≥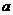 <2
D.
<2
D.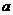 >2
>2
3.下列说法中,正确的是( )
A.等腰梯形既是中心对称图形又是轴对称图形
B.正方形的对角线互相垂直平分且相等
C.矩形是轴对称图形且有四条对称轴
D.菱形的对角线相等
4.下列事件发生的概率为0的是( ).
A.随意掷一枚均匀的硬币两次,至少有一次反面朝上
B.今年冬天黑龙江会下雪
C.一个转盘被分成6个扇形,按红、白、白、红、红、白排列,转动转盘,指针停在红色区域
D.随意掷两个均匀的骰子,朝上面的点数之和为1
5.将一正方形纸片按下列顺序折叠,然后将最后折叠的纸片沿虚线剪去上方的小三角形.将纸片展开,得到的图形是( )


A B C D
二、填空题(本大题共5小题,每小题4分,共20分)请把下列各题的正确答案填写在横线上.
6.将4个数a.b.c.d排成2行、2列,两边各加一条竖直线记成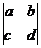 定义
定义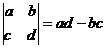 ,叫做2阶行列式.若
,叫做2阶行列式.若 =6则
=6则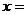 ________.
________.
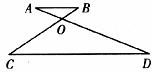
7.如图,AB∥CD,AB/CD=1/3,△COD的周长
8.边长为
9.学校团委组织九年级的共青团员参加植树活动,七个团支部植树的棵数为:16,13,15,16,14,17,17,则这组数据的中位数是________.
10.将一个正三角形纸片剪成四个全等的小正三角形,再将其中的一个按同样的方法剪成四个更小的正三角形,……如此继续下去,结果如下表:
所剪次数
1
2
3
4
…
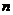
正三角形个数
4
7
10
13
…
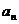
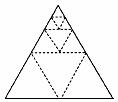
则________ (用含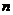 的代数式表示).
的代数式表示).
三、解答题(本大题共5小题,每小题6分,共30分)
11.计算: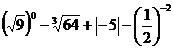
12.先化简,再求值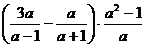 ,其中
,其中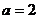 .
.
13.解方程: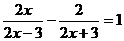
14.如图,AB为⊙O的直径,D为弦BE的中点,连接OD并延长交⊙O于点F,与过B点的切线相交于点C.若点E为弧AF的中点,连接AE
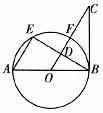
求证:△ABE≌△OCB.
15.某市2008年秋季落实减免学生在义务教育阶段的学杂费政策,按照每学期小学每个学生250元、初中每个学生450元的标准,由财政拨付学校作为办公经费.该市一学校小学生和初中生共有840人,2008年秋季收到当学期该项拨款290000元,该学校小学生和初中生各有多少人?
四、解答题(本大题共4小题,每小题7分,共28分)
16.为积极响应党中央关于支援“5? 顶帐篷.生产过程中的剩余生产任务y(顶)与已用生产时间
顶帐篷.生产过程中的剩余生产任务y(顶)与已用生产时间 (时)之问的关系如图所示.
(时)之问的关系如图所示.
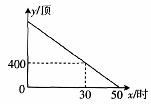
(1)求变量y与 之间的关系式.
之间的关系式.
(2)求m的值.
17.如图(1),有四张编号为1,2,3,4的卡片,卡片的背面完全相同,现将它们洗匀并正面朝下放置在桌面上.
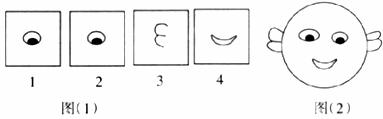
(1)从中随机抽取一张,抽到的卡片是眼睛的概率是多少?
(2)从四张卡片中随机抽取一张贴在如图(2)所示的大头娃娃的左眼处,然后再随机抽取一张贴在大头娃娃的有眼处,用树状图或列表法求贴法正确的概率.
18.根据指令[s,A](s≥0,00<A<1800),机器人在平面上能完成下列动作:先原地逆时针旋转角度A,再朝其面对的方向沿直线行走距离s.现机器人在直角坐标系的坐标原点,且面对 轴正方向.
轴正方向.
(1)若给机器人下了一个指令[4,600],求机器人应移到的位置.
(2)请你给机器人下一个指令,使其移到点(-5,5).
19.2008年4月,国民体质监测中心等机构开展了青少年形体测评.专家组随机抽查了某市若干名初中学生坐姿、站姿、走姿的好坏情况.我们对专家的测评数据作了适当处理(如果一个学生有一种以上不良姿势,我们以他最突出的一种作记载),并将统计结果绘制了如下两幅不完整的统计图,请你根据图中所给信息解答下列问题:
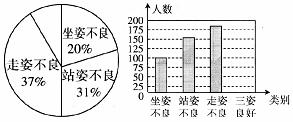
(1)在这次被抽查的学生中,坐姿不良的学生有_______人,占抽查人数的百分比为_______,这次一共抽查了_______名学生;如果全市有7万名初中生,那么全市初中生中,三姿良好的学生约有_______人.
(2)请将两幅统计图补充完整.
(3)根据统计结果,请你简单谈谈自己的看法.
五、解答题(本大题共3小题,每小题9分,共27分)
20.如图所示,在边长都是1的正方形网格中有一个鸟形图案.
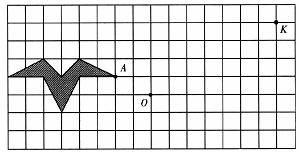
(1)求出这个鸟形图案所占的面积.
(2)把它平移,使点A落在点K处,请作出平移后的鸟形图案,并写出两种不同的平移路线.
(3)把它以O点为中心旋转1800,请作出旋转后的鸟形图案.
①方程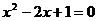 的根是
的根是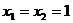 ,则有
,则有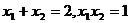 ;
;
②方程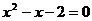 的根是
的根是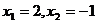 ,则有
,则有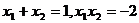 ;
;
③方程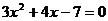 的根是
的根是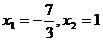 ,则有
,则有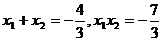
(1)根据以上①②③请你猜想:如果关于 的一元二次方程
的一元二次方程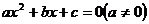 有两个实数根为
有两个实数根为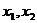 ,那么
,那么 与系数
与系数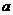 、b、
、b、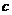 有什么关系?请写出你的猜想并证明你的猜想.
有什么关系?请写出你的猜想并证明你的猜想.
(2)利用你的猜想结论,解决下面的问题:
已知关于 的方程
的方程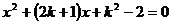 有实数根
有实数根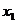 、
、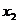 ,且
,且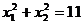 ,求k的值.
,求k的值.
22.如图,在Rt△ABC中,AB=AC,P是边AB(含端点)上的动点.过P作BC的垂线PR,R为垂足,∠PRB的平分线与AB相交于点S,在线段RS上存在一点T,若以线段PT为一边作正方形PTEF,其顶点E、F恰好分别在边BC、AC上.
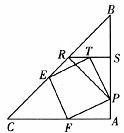
(1)△ABC与△SBR是否相似,说明理由.
(2)请你探索线段TS与PA的长度之间的关系.
(3)设边AB=1,当P在边AB(含端点)上运动时,请你探索正方形PTEF的面积y的最小值和最大值.