2009年江苏新课标相似图形测试（A卷）
数学试卷
一、精心选一选．（每题3分，共30分）
1．已知2
=3y=4z，则：y：z是 （ ）
A．2：3：4 B．4：3：
2．在比例尺为1：8000的南京市城区地图上，太平南路的长度约为
A．
3．有四组线段，每组线段长度如下，能组成比例（排列顺序可调换）的有 （ ）
①2，1，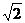
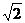， ②3，2，6，4 ③
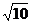，1，
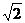， ④1，3，5，7
A．1组 B．2组 C．3组 D．4组
4．下列命题中，正确的个数是 （ ）
①两个直角三角形是相似三角形 ②两个等腰三角形是相似三角形 ③两个等腰直角三角形是相似三角形 ④等边三角形是相似三角形
A．4个 B．3个 C．2个 D．1个
5．两个相似三角形的相似比是3：5，较大三角形的最小边长为
A．
6．如图，已知△ABC，P是AB边上的一点，连结CP，下列条件不能判定△ACP∽△ABC的是 （ ）
A．∠ACP=∠B B．∠APC=∠ACB
C．AC2=AP?AB
D．
7．在Rt△ABC中，斜边AB上的高为CD，AB=12，AD：BD=3：1，那么CD长为（ ）
A．6 B．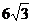
C．18
D．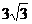
8．如图，DE／／FG／／BC，图中相似三角形共有几对 （ ）
A．1 B．
9．张华的身高为
A．3．
10．如下图，在四边形ABCD中，E是对角线BD上的一点，EF//AB，EM//CD，则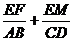
的值为 （
）
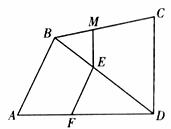
A．2 B．0．
二、耐心填一填．（每题2分，共20分）
11．已知
，且
，求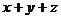
=__________。
12．延长线段AB到C，使BC=AB，则AC：AB=_________，AB：BC=_________，BC：AC=_________．
13．在比例尺为1：500000的地图上，量得甲、乙两地的距离是
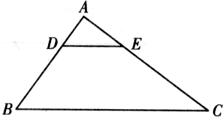
14．如图，在△ABC中，DE//BC，AD=2，AE=3，BD=4，则AC=_________。
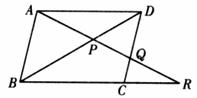
15．如图，在平行四边形ABCD中，R在BC的延长线上，AR交BD于P，交CD于Q，若DQ：CQ=4：3，则AP：PR=_________．
16．如图，点D是△ABC内一点，连结BD并延长到E，连结AD、AE，若∠BAD=20°，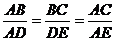
，则∠EAC=_________
17．在△ABC中，DE//BC，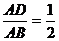
，且S△ABC=
18．把一个三角形变成和它相似的三角形，而面积扩大为原来的l00倍，则边长扩大为原来的_________倍．
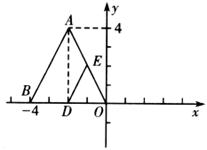
19．如下图，△EDO是△ABO缩小后得到的，则点E的坐标为__________________。
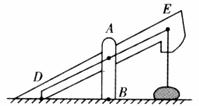
20．如下图所示为农村一古老的捣碎器，已知支撑柱AB的高为
三、用心想一想．（共50分）
21．（8分）如图，△AEB和△FEC是否相似?
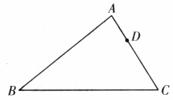
22．（8分）如图，在△ABC中，AB=8，AC=6，点D在AC上，AD=2，试在AB上求一点E，使△ADE和△ABC相似，并求出AE的长．
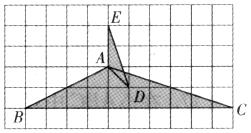
23．（8分）在边长为1的正方形网格中有A、B、C、D、E五个点，问△ABC与△ADE是否相似?为什么?由此，你还能找出图中相似的三角形吗?若能，请找出来，并说明理由．
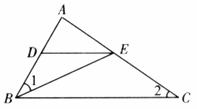
24．（8分）如图，AE2=AD?AB，且∠ABE=∠C，试说明△BCE∽△EBD．
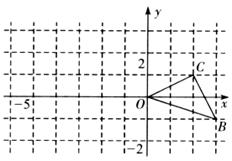
25．（8分）如图，已知O是坐标原点，B、C两点的坐标分别为（3，一l）、（2，1）．
（1）以D点为位似中心在y轴的左侧将△OBC放大到两倍（即新图与原图的相似比为2），画出图形；
（2）分别写出B、C两点的对应点B’、C’的坐标；
（3）如果△OBC内部一点M的坐标为（，y），写出M的对应点M’的坐标．
26．（10分）如图，已知Rt△ABC与Rt△DEF不相似，其中∠C、∠F为直角，能否分别将这两个三角形各分割成两个三角形，使△ABC分成的两个三角形与△DEF所分成的两个三角形分别对应相似?如果能，请你设计出一种分割方案．
