2008-2009学年度重庆市西南师大附中第二学期初二期末考试
数学试卷
一、选择题(每小题4分,共40分)
1. 一元二次方程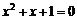 的根的情况是( )
的根的情况是( )
A.只有一个实数根 B.有两个相等的实数根
C.有两个不相等的实数根 D.没有实数根
2. 若y=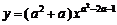 是二次函数,那么( )
是二次函数,那么( )
A.a=-1或a=3 B.a≠-1且a≠0
C.a=-1 D.a=3
3. 若点(3,6)在反比例函数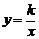 (k≠0)的图象上,那么下列各点在此图象上的是( )
(k≠0)的图象上,那么下列各点在此图象上的是( )
A.(-3,6) B.(2,9) C.(2,-9) D.(3,-6)
4. 在三角形ABC中,若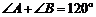 ,则sinC等于( )
,则sinC等于( )
A.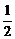 B.
B.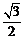 C.
C.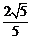 D.
D.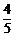
5. 抛物线y=2x2-4x+7的顶点坐标是( )
A.(-1,13) B.(-1,5) C.(1,9) D.(1,5)
6. 将一个二次函数图像向下平移2个单位,再向左平移3个单位,所得到的函数图像解析式为y=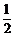 x2,则这个函数的解析式为( )
x2,则这个函数的解析式为( )
A.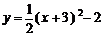 B.
B.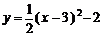
C.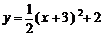 D.
D.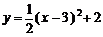
7. 已知:k=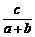 =
=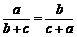 ,则k的值是( )
,则k的值是( )
A.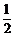 B.-
B.-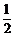 或-1
或-1
8. 将一个各面涂有颜色的正方体,分割成同样大小的27个小正方体,从这些正方体中任取一个,恰有3个面涂有颜色的概率是( )
A.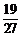 B.
B.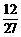 C.
C.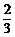 D.
D.
9. 如图,已知DE∥BC,CE和BD相交于点O,S△DOE∶S△COB=4∶9,则AE∶EB为( )
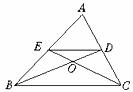
A.2∶1 B.2∶
10. 如图,在直角梯形ABCD中,DC∥AB,∠A = 90°,AB =
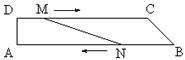
二、填空题(每小题4分,共32分)
11. 在标号为1、2、3……19的19个同样的小球中任选一个,则选中标号为偶数的小球的可能性______________选中标号为奇数的小球的可能性。(填“>”、“=”、“<”符号)
12. 已知线段a=
13. 若抛物线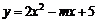 的对称轴方程为
的对称轴方程为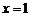 ,则
,则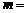 .
.
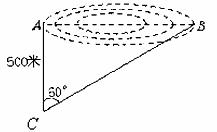
14. 某风景区改造中,需测量湖两岸游船码头A、B间的距离,设计人员由码头A沿与AB垂直的方向前进了
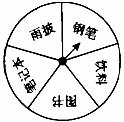
15. 某单位的联欢会上,设有一个摇奖节目,奖品为雨披,钢笔,饮料,图书,笔记本,标于一个转盘的相应区域上(转盘被均匀等分为五个区域,如图)。转盘可以自由转动,参与者转动转盘,当转盘停止时,指针落在哪一个区域,就获得哪种奖品,则获得钢笔的概率为 .
16. 已知一组数据x1,x2,x3,x4,x5的平均数是2,,那么另一组数据3x1-2,3x2-2,3x3-2,3x4-2,3x5-2的平均数是 .
17. 若A(x1,y1),B(x2,y2),C(x3,y3)都是反比例函数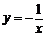 的图象上的点,且x1<0<x2<x3,则y1,y2,y3由小到大的顺序是 .
的图象上的点,且x1<0<x2<x3,则y1,y2,y3由小到大的顺序是 .
18. 已知二次函数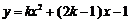 与x轴交点的横坐标为
与x轴交点的横坐标为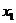 ,
,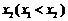 ,则对于下列结论:
,则对于下列结论:
①当x=-2时,y=1
②当x>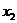 时,y>0
时,y>0
③方程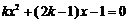 有两个不相等的实数根
有两个不相等的实数根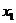 ,
,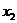
④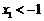 ,
,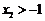
⑤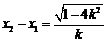
其中所有正确的结论是_______________(只须填写序号).
三、计算或解方程(每小题4分,共16分)
19.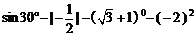 20.
20.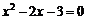
21.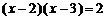 22.
22.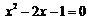
四、解答题(每小题8分,共32分)
23.当m为何值时,关于x方程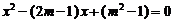 有两个相等的实数根,并求出这时方程的根。
有两个相等的实数根,并求出这时方程的根。
24.甲、乙两人在相同条件下各射靶10次,每次射靶的成绩情况如图所示.
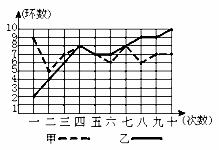
(1)请填写下表:
平均数
方差
中位数
命中9环及以上次数
甲
7
1.2
乙
5.4
7.5
(2)请从下列四个不同的角度对这次测试结果进行分析:
①从平均数和方差相结合看(分析谁的成绩更稳定);
②从平均数和中位数相结合看(分析谁的成绩更好些);
③从平均数和命中9环及以上的次数相结合看(分析谁的成绩更好些);
④从折线图上两人射击命中环数的走势看(分析谁更有潜力).
25.已知正比例函数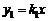 和反比例函数
和反比例函数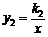 的图像的一个交点为A(2,-1),求这两个函数的解析式。并求它们的另一个交点B的坐标。
的图像的一个交点为A(2,-1),求这两个函数的解析式。并求它们的另一个交点B的坐标。
26.对于气温,通常有摄氏温度和华氏温度两种表示,且两者之间存在着某种函数关系,下列给出了摄氏(℃)温度x与华氏(°F)温度y之间对应关系.
x(℃)
…
-10
0
10
20
30
…
y(°F)
…
14
32
50
68
86
…
(1)通过①描点、连线;②猜想;③求解;④验证等几个步骤,试确定y与x之间的函数关系式;
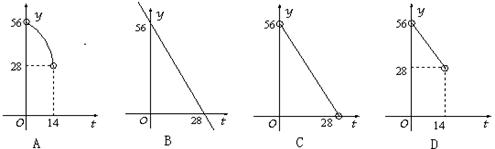
(2)某天,沈阳的最高气温是

五、解答题(每小题10分,共30分)
27.某超市为了吸引顾客,规定:凡购买50元以上的物品的顾客均可获奖,可以直接获得购物券5元,也可以参加摸奖。摸奖的方法是:从一个装有50个彩球的盒子中任取一球,摸到红球可获50元的购物券;摸到黄、篮球,可分别获30,10元的购物券,而摸到白球,不能获奖。已知50个球中,3个红球,5个黄球,10个篮球,其余均为白球。现有一位顾客决定参加摸奖,你认为他这种选择合算吗?为什么?
28.已知:如图,□ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE、BF相交于H,BF、AD的延长线相交于G.
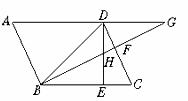
求证:(1) AB=BH;
(2) AB2=GA?HE.
29.如图,抛物线y=ax2+bx+c与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,且当x=0和x=2时,y的值相等。直线y=3x - 7与这条抛物线相交于两点,其中一点的横坐标是4,另一点是这条抛物线的顶点M.
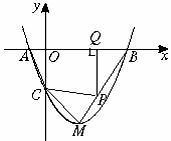
(1)求这条抛物线的解析式;
(2)P为线段BM上一点,过点P向x轴引垂线,垂足为Q.若点P在线段BM上运动(点P不与点B、M重合),设OQ的长为t,四边形PQAC的面积为S.求S与t之间的函数关系式及自变量t的取值范围;
(3)在线段BM上是否存在点N,使△NMC为等腰三角形?若存在,请求出点N的坐标;若不存在,请说明理由。