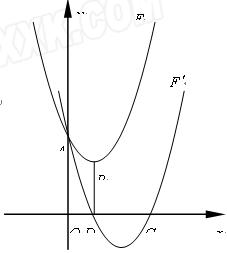
摘要：29．如图.抛物线y＝ax2+bx+c与x轴交于A.B两点(点A在点B左侧).与y轴交于点C.且当x＝0和x＝2时.y的值相等.直线y＝3x - 7与这条抛物线相交于两点.其中一点的横坐标是4.另一点是这条抛物线的顶点M．
网址：http://m.1010jiajiao.com/timu_id_771648[举报]
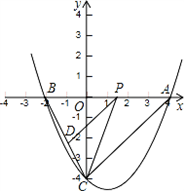
如图，抛物线y＝ax2＋bx－4与x轴交于A(4，0)、B(
－2，0)两点，与y轴交于点C，点P是线段AB上一动点(端点除外)，过点P作PD∥AC，交BC于点D，连接CP．
(1)求该抛物线的解析式；
(2)当动点P运动到何处时，BP2＝BD·BC；
(3)当△PCD的面积最大时，求点P的坐标．
－2，0)两点，与y轴交于点C，点P是线段AB上一动点(端点除外)，过点P作PD∥AC，交BC于点D，连接CP．(1)求该抛物线的解析式；
(2)当动点P运动到何处时，BP2＝BD·BC；
(3)当△PCD的面积最大时，求点P的坐标．
如图，抛物线y＝ax2＋bx＋c经过原点O，与x轴交于另一点N，直线y＝kx＋4与两坐标轴分别交于A、D两点，与抛物线交于点B(1，m)、C(2，2)．
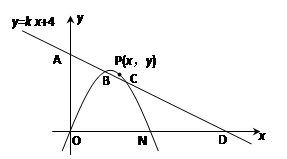
1.求直线与抛物线的解析式．
2.若抛物线在x轴上方的部分有一动点P(x，y)，设∠PON＝
，求当△PON的面积最大时tan的值．
3.若动点P保持（2）中的运动线路，问是否存在点P，使得△POA的面积等于△PON的面积的？若存在，请求出点P的坐标；若不存在，请说明理由
查看习题详情和答案>>
如图，抛物线y＝ax2＋bx＋c经过原点O，与x轴交于另一点N，直线y＝kx＋4与两坐标轴分别交于A、D两点，与抛物线交于点B(1，m)、C(2，2)．
【小题1】求直线与抛物线的解析式．
【小题2】若抛物线在x轴上方的部分有一动点P(x，y)，设∠PON＝
，求当△PON的面积最大时tan的值．
【小题3】若动点P保持（2）中的运动线路，问是否存在点P，使得△POA的面积等于△PON的面积的？若存在，请求出点P的坐标；若不存在，请说明理由 查看习题详情和答案>>
【小题1】求直线与抛物线的解析式．
【小题2】若抛物线在x轴上方的部分有一动点P(x，y)，设∠PON＝
，求当△PON的面积最大时tan的值．【小题3】若动点P保持（2）中的运动线路，问是否存在点P，使得△POA的面积等于△PON的面积的？若存在，请求出点P的坐标；若不存在，请说明理由 查看习题详情和答案>>
轴交于点A，
的值；
