网址:http://m.1010jiajiao.com/timu_id_771605[举报]
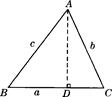
观察与思考:阅读下列材料,并解决后面的问题.在锐角△ABC中,∠A、∠B、∠C的对边分别是a、b、c,过A作 AD⊥BC于D(如图),则sinB=![]() ,sinC=
,sinC=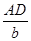 ,即AD=csinB,AD=bsinC,于是csinB=bsinC,即
,即AD=csinB,AD=bsinC,于是csinB=bsinC,即![]() .同理有:
.同理有:![]() ,
,![]() ,所以
,所以![]()
即:在一个三角形中,各边和它所对角的正弦的比相等.在锐角三角形中,若已知三个元素(至少有一条边),运用上述结论和有关定理就可以求出其余三个未知元素.根据上述材料,完成下列各题.
1.如图,△ABC中,∠B=450,∠C=750,BC=60,则∠A= ;AC= ;
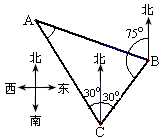
2.如图,一货轮在C处测得灯塔A在货轮的北偏西30°的方向上,随后货轮以60海里/时的速度按北偏东30°的方向航行,半小时后到达B处,此时又测得灯塔A在货轮的北偏西75°的方向上(如图),求此时货轮距灯塔A的距离AB.
查看习题详情和答案>>
 ,sinC=
,sinC= ,即AD=csinB,AD=bsinC,于是csinB=bsinC,即
,即AD=csinB,AD=bsinC,于是csinB=bsinC,即 .同理有:
.同理有: ,
, ,所以
,所以
即:在一个三角形中,各边和它所对角的正弦的比相等.在锐角三角形中,若已知三个元素(至少有一条边),运用上述结论和有关定理就可以求出其余三个未知元素.根据上述材料,完成下列各题.
【小题1】如图,△ABC中,∠B=450,∠C=750,BC=60,则∠A= ;AC= ;
【小题2】如图,一货轮在C处测得灯塔A在货轮的北偏西30°的方向上,随后货轮以60海里/时的速度按北偏东30°的方向航行,半小时后到达B处,此时又测得灯塔A在货轮的北偏西75°的方向上(如图),求此时货轮距灯塔A的距离AB.
 查看习题详情和答案>>
查看习题详情和答案>>
观察与思考:阅读下列材料,并解决后面的问题.在锐角△ABC中,∠A、∠B、∠C的对边分别是a、b、c,过A作 AD⊥BC于D(如图),则sinB= ,sinC=
,sinC= ,即AD=csinB,AD=bsinC,于是csinB=bsinC,即
,即AD=csinB,AD=bsinC,于是csinB=bsinC,即 .同理有:
.同理有: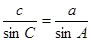 ,
, ,所以
,所以
即:在一个三角形中,各边和它所对角的正弦的比相等.在锐角三角形中,若已知三个元素(至少有一条边),运用上述结论和有关定理就可以求出其余三个未知元素.根据上述材料,完成下列各题.
【小题1】如图,△ABC中,∠B=450,∠C=750,BC=60,则∠A= ;AC= ;
【小题2】如图,一货轮在C处测得灯塔A在货轮的北偏西30°的方向上,随后货轮以60海里/时的速度按北偏东30°的方向航行,半小时后到达B处,此时又测得灯塔A在货轮的北偏西75°的方向上(如图),求此时货轮距灯塔A的距离AB.

观察与思考:阅读下列材料,并解决后面的问题.在锐角△ABC中,∠A、∠B、∠C的对边分别是a、b、c,过A作 AD⊥BC于D(如图),则sinB=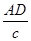 ,sinC=
,sinC=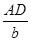 ,即AD=csinB,AD=bsinC,于是csinB=bsinC,即
,即AD=csinB,AD=bsinC,于是csinB=bsinC,即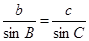 .同理有:
.同理有: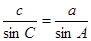 ,
,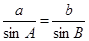 ,所以
,所以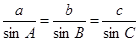
即:在一个三角形中,各边和它所对角的正弦的比相等.在锐角三角形中,若已知三个元素(至少有一条边),运用上述结论和有关定理就可以求出其余三个未知元素.根据上述材料,完成下列各题.
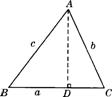
1.如图,△ABC中,∠B=450,∠C=750,BC=60,则∠A= ;AC= ;
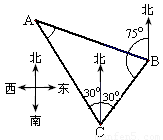
2.如图,一货轮在C处测得灯塔A在货轮的北偏西30°的方向上,随后货轮以60海里/时的速度按北偏东30°的方向航行,半小时后到达B处,此时又测得灯塔A在货轮的北偏西75°的方向上(如图),求此时货轮距灯塔A的距离AB.
查看习题详情和答案>>