2009-2010学年度沧州市颐和中学第一学期九年级第一次月考
数学试卷
考试时间:120分钟 满分:120分
一.选择题(每小题3分,共27分)
1.使式子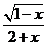 有意义的
有意义的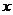 的取值范围是( )
的取值范围是( )
A.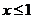 B.
B.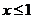 且
且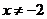
C.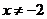 D.
D.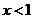 且
且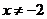
2.下列各式中计算正确的是( )
A.
B.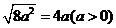
C.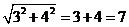
D.
3.已知直角三角形的一条直角边9,斜边长为10,则另一条直角边为( )
A.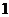 B.
B.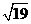 C.
C. D.
D.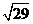
4.关于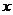 的方程
的方程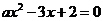 是一元二次方程,则( )
是一元二次方程,则( )
A.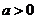 B.
B.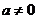 C.
C.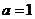 D.
D.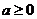
5、用配方法解下列方程时,配方有错误的是( )
A.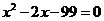 化为
化为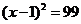
B. 化为
化为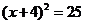
C.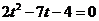 化为
化为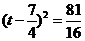
D.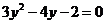 化
化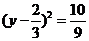
6.方程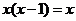 的根是 ( )
的根是 ( )
A.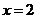 B.
B.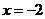 C.
C.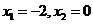 D.
D.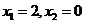
7.若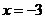 ,则
,则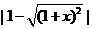 ( )
( )
A.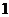 B.
B.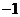 C.
C. D.
D.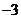
8.再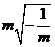 根号外的因式移入根号内得( )
根号外的因式移入根号内得( )
A.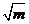 B.
B.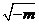 C.
C.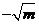 D.
D.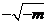
9.某市化肥厂第一季度生产化肥100万吨,以后每季度比上一季度增产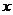 (增长率),前三季度共生产化肥360万吨,则下列方程正确的是 ( )
(增长率),前三季度共生产化肥360万吨,则下列方程正确的是 ( )
A.100(1+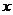 )=360
B.100(1+
)=360
B.100(1+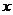 )
)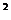 =360
=360
C.100+100(1+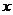 )+100(1+
)+100(1+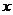 )
)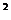 =360 D.100+100(1+
=360 D.100+100(1+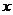 )
)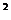 =360
=360
二.填空题:(每小题3分,共21分)
10.使式子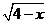 无意义的
无意义的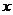 的取值范围是____________
的取值范围是____________
11.若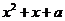 是完全平方式,则
是完全平方式,则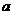 =_____________
=_____________
12.化简: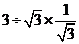 =________________
=________________
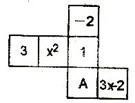
13.如图是一个正方体的展开图,标注了字母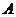 的面是正方体的正面,如果正方体的左面与右面所标注代数式的值相等,则
的面是正方体的正面,如果正方体的左面与右面所标注代数式的值相等,则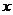 的值是_________
的值是_________
14.已知一个三角形的两边长分别是方程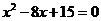 ,则第三边y的取值范围是________
,则第三边y的取值范围是________
15.某毕业班数学活动小组的同学互送相片作记念,已知全班共送出相片132张,则该活动小组有_____________人。
16.一个两位数,个位数字比十位数字大3,个位数字的平方刚好等于这个两位数,则这个两数是______________。
三.计算:(每小题6分,共12分)
17.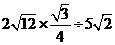 18.
18.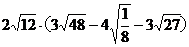
四.解方程:(每小题6分,共12分)
19.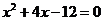 (用配方法) 20.
(用配方法) 20.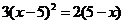
五.解答题
21.己知: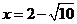 ,求代数式
,求代数式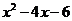 的值。(8分)
的值。(8分)
22.一张桌子的桌面长为
23.百货商店服装专柜在销售中发现:某品牌童装平均每天可销售20件,每件盈利40元。为迎“六一”国际儿童节,商店决定采取降价的措施,扩大销售量,增加盈利,减少库存,经市场调查发现,如果每件童装降价1元,那么平均每天就可多售出2件,要想平均每天销售这种童装盈利1200元,那么每件童装应降价多少元?(10分)
24.美化城市,改善人们的居住环境已成为城市建设的一项重要内容,某城区儿年来,通过拆迁旧房、植草、栽树、修建公园等措施,使城区绿地面积不断增加(如图所示)。(10分)
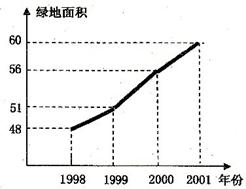
(1)根据图中所提供的信息,回答下列问题:
2001年的绿地面积为________公顷,比2000年增加了________公顷,在1999年,2000年,2001年这三年中,绿地面积增加最多的是_______________年。
(2)为满足城市发展的需要,计划2003年使城区绿地面积达到72.
25.如图所示:在直角坐标系中,四边形OABC为矩形,B点的坐标(3,6),若点P从点O沿OA向点A以每秒1个单位长度的速度运动,点Q从点A沿AB以每秒2个单位长度的速度运动,如果P、Q分别从O、A同时出发,当其中一点到达终点时,另一点也随之停止运动,假设运动的时间为T秒,请解答下列问题
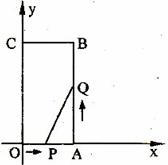
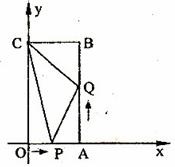
图1 图2
(1)如图1所示:用含有T的代数式表示 的面积(3分)
的面积(3分)
(2)如图1所示:当T为何值时,线段PQ的长度为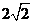 ?(3分)
?(3分)
(3)如图2所示:当T为何值时,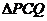 为等腰三角形?(6分)
为等腰三角形?(6分)