2008-2009学年度山东省临沂市费县第二学期八年级学业水平检测
数学试卷
一、选择题 本大题共10小题,请将每小题唯一正确答案的代号填在表格内。
1.使式子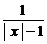 有意义的
有意义的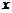 的取值范围为
的取值范围为
A.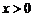 B.
B.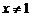 C.
C.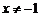 D.
D.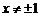
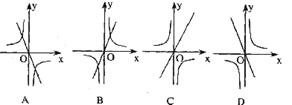
2.如图所示,正比例函数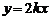 与反比例函数
与反比例函数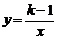 在同一坐标系中的图象不可能是
在同一坐标系中的图象不可能是
3.若一组数据1,2,3,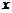 的极差为6,则
的极差为6,则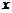 的值是
的值是
A.7 B.
4.化简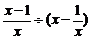 的结果为
的结果为
A.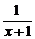 B.
B.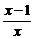 C.
C.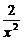 D.
D.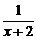
5.如图,点P是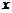 轴上的一个动点,过点P作
轴上的一个动点,过点P作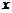 轴的垂线,交双曲线
轴的垂线,交双曲线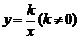 于点Q,当点P沿
于点Q,当点P沿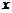 轴正半轴方向运动时,Rt△POQ的面积变化情况为
轴正半轴方向运动时,Rt△POQ的面积变化情况为
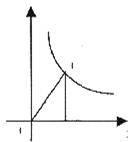
A.逐渐增大 B.逐渐减小 C.保持不变 D.无法确定
6.一架25分米长的梯子,斜立在一竖直的墙上,这时梯足距离墙底端7分米,如果梯子的顶端沿墙下滑4分米,那么梯足将滑动
A.9分米 B.15分米 C.5分米 D.8分米
7.在△ABC中,∠A,∠B,∠C的对边分别为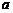 ,
,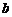 ,
,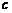 ,且
,且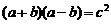 ,则
,则
A.∠A为直角 B.∠C为直角
C.∠B为直角 D.不是直角三角形
8.用两个边长为a的等边三角形纸片拼成的四边形是
A.等腰梯形 B.正方形 C.矩形 D.菱形
9.如下图,在等腰梯形ABCD中,AD∥BC,AC、BD相交于点O,则图中全等三角形共有
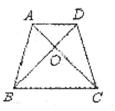
A.1对 B.2对 C.3对 D.4对
10.四边形ABCD中,AC、BD相交于点O,能判别这个四边形是正方形的条件是
A.OA=OB=OC=OD,AC⊥BD B.AB∥CD,AC=BD
C.AD∥BC,∠A=∠C D.OA=OC,OB=OD,AB=BC
二、填空题:请将正确答案直接填在题中横线上。
11.如图,四边形ABCD是平行四边形,AD=12,AB=13,BD⊥AD,则OB的长为_______。
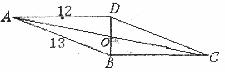
12.等腰梯形下底与上底的差等于一腰的长;那么腰与下底的夹角是_______。
13.已知二组数据10,10,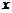 ,8的平均数为10,则这组数据的中位数为_______。
,8的平均数为10,则这组数据的中位数为_______。
14.填空: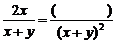 。
。
15.不改变分式的值,把式子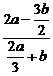 中的分子与分母中的各项系数都化为整数为_______。
中的分子与分母中的各项系数都化为整数为_______。
16.若反比例函数 的图象位于一、三象限内,正比例函数
的图象位于一、三象限内,正比例函数 过二、四象限,则
过二、四象限,则 的整数值是_______。
的整数值是_______。
17.在矩形ABCD的边AB上有一点E,且CE=DE,若;AB=2AD,则∠ADE等于_______。
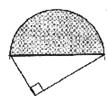
18.如下图,直角三角形的两直角边长分别为6和8,则以斜边为直径的半圆的面积是_______。
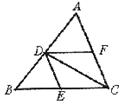
19.如下图,△ABC中,CD平分∠ACB AB于D,DE∥AC交BC于E,DF∥BC交AC于F,则四边形DECF的形状是_________。(写出的图形要充分利用已知条件)
20.已知数据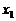 ,
,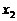 ,
,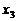 ,
,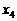 ,…,
,…,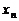 的平均数是5,方差为2,则
的平均数是5,方差为2,则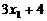 ,
,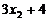 ,……,
,……,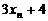 的平均数是_________,方差是__________。
的平均数是_________,方差是__________。
三、解答题
21.
22.某商场出售一批进价为2元的贺卡,在商场营销中发现此商品的日销售单价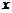 元与销售量
元与销售量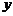 个之间有如下关系:
个之间有如下关系:
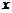 (元)
(元)
3
4
5
6
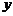 (个)
(个)
20
15
12
10
(1)根据表中的数据在直角坐标系中描出实数对(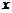 ,
,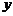 )的对应点并连线;
)的对应点并连线;
(2)猜测并确定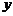 与
与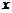 之间的函数关系式;
之间的函数关系式;
(3)当日销售单价为10元时,贺卡的日销售量是多少个?
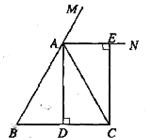
23.如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,求证:四边形ADCE为矩形。
24.如图,某单位欲从内部选拔管理人员一名,对甲、乙、丙三名候选人进行了笔试和面试两项测试,三人的测试成绩如下表所示:
测试
测试成绩/分
项目
甲
乙
丙
笔试
75
80
90
面试
93
70
68
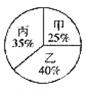
根据录用程序,组织200名职工对三人利用投票推荐的方式进行民主评议,三人得票率(没有弃权票,每位职工只能推荐1人)如扇形图所示,每得一票记作1分。
(1)请算出三人的民主评议得分;
(2)如果根据三项测试的平均成绩确定录用人选,那么谁将被录用(精确到0.01)?
(3)根据实际需要,单位将笔试、面试、民主评议三项测试得分按4∶3∶3的比例确定个人成绩,那么谁将被录用?
25.如图所示,公路MN和公路PQ在P点处交汇,点A处有一所中学,AP=
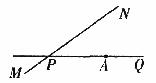
26.如图,等腰梯形ABCD中,AD∥BC,AB=DC。点E是线段AD上的一个动点(E与A,D不重合),G,F,H分别是BE,BC,CE的中点。
(1)试探索四边形EGFH的形状,并说明理由;
(2)当点E运动到什么位置时,四边形EGFH是菱形?并加以证明;
(3)若(2)申的菱形EGFH是正方形;请探索线段EF与线段BC的关系,并证明你的结论。
