2008-2009学年度广东省汕头市金平区第二学期初二教学质量考试
数学试卷
(满分150分,考试时间100分钟)
卷首语:没有比人更高的山,没有比脚更长的路,亲爱的同学请相信自己,沉着应答,你一定能愉快地完成这次测试之旅,祝你成功!
一、相信你,都能选择对!四个选项中只有一个是正确的,请将正确答案代号填在各题相应题号后的括号里。(每题4分,共32分)
1.函数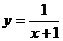 中,自变量x的取值范围是( )
中,自变量x的取值范围是( )
A.x≠-l B.x
>
2.小明在下面的计算中,有一道题做对了,则他做对的题目是( )
A.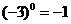 B.
B. C.
C.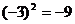 D.
D.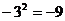
3.为筹备班级的初中毕业联欢会, 班长对全班同学爱吃哪几种水果作民意调查, 从而最终决定买什么水果。下列调查数据中最值得关注的是( )
A.平均数 B.中位数 C.众数 D.方差
4.平行四边形ABCD中,如果∠A=55°,那么∠C的度数是( )
A.45° B.55° C.125° D.145°
5.若双曲线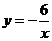 经过点A(
经过点A(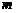 ,3),则
,3),则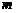 的值为( )
的值为( )
A.2 B.-
6.根据物理学家波义耳1662年的研究结果:在温度不变的情况下,气球内气体的压强p(pa)与它的体积v(m3)的乘积是一个常数k,即pv=k(k为常数,k>0),下列图象能正确反映p与v之间函数关系的是( )。
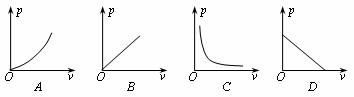
7.一个三角形的三边长分别为6,8,10,则这个三角形一定是( )
A.锐角三角形 B.直角三角形 C.钝角三角 D.以上答案都不对
8.如下图,将一块边长为12的正方形纸片ABCD的顶点A折叠至DC边上的点E,使DE=5,折痕为PQ,则PQ的长为( )
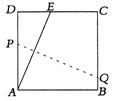
A.15
B.
二、希望你能填得又快又准。(每题4分,共20分) 8题图
9.2005年新版人民币中一角硬币的直径约为
10.现有甲、乙两支球队,每支球队队员身高数据的平均数均为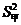 = 0.28、
= 0.28、 = 0.36,则身高较整齐的球队是
队(填“甲”或“乙” ).
= 0.36,则身高较整齐的球队是
队(填“甲”或“乙” ).
11.如下图,若D,E分别是AB,AC中点,现测得DE的长为
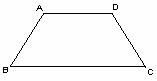
12.如图,等腰梯形ABCD中,AD‖BC,∠A=130°,则∠C=__________度。
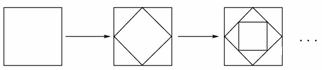
13.如图,依次连结一个边长为1的正方形各边的中点,得到第二个正方形,再依次连结第二个正方形各边的中点,得到第三个正方形,按此方法继续下去, 则第六个正方形的面积是 .
三、讲究方法,得心应手。(每题7分,共35分)
14.请将式子: ×(1+
×(1+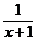 )化简后,再从0,1,2三个数中选择一个你喜欢且使原式有意义的x的值代入求值。
)化简后,再从0,1,2三个数中选择一个你喜欢且使原式有意义的x的值代入求值。
15.解分式方程:
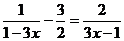
16.一司机驾驶汽车从甲地去乙地,以80千米/小时的平均速度用4小时到达目的地。
(1)当他按原路匀速返回时,求汽车速度v(千米/小时)与时间t(小时)之间的函数关系式;
(2)如果该司机匀速返回时,用了3.2小时,求返回时的速度。
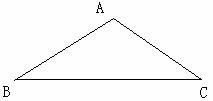
17.如图,△ABC中,AB=AC=13,BC=24,请你建立适当的直角坐标系,并直接写出A,B,C各点的坐标。
18.水资源越来越缺乏,全球提倡节约用水。本市水厂为了了解某小区居民的用水情况,随机抽查了该小区10户家庭的月用水量,有关数据如下表:
月用水量(m3)
10
13
14
17
18
户数
2
2
3
2
1
(1)在这个统计中,众数是 ,中位数是 ;这10户家庭该月平均用水量是 ;
(2)如果该小区有500户家庭,根据上面的计算结果,估计该小区居民每月需要用水多少立方米?
四、圆满的解答,相信你一定表现出色(每题9分,共27分)
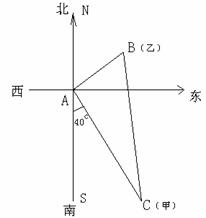
19.如图,甲、乙两船从港口A同时出发,甲船以16海里/小时的速度向南偏东40°的方向航行,乙船以
20.某运输公司准备运输一批货物,需要的货船数量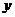 (艘)与货船的核定装载量
(艘)与货船的核定装载量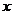 (吨)之间的函数关系如图所示,请根据图像提供的信息回答问题:
(吨)之间的函数关系如图所示,请根据图像提供的信息回答问题:
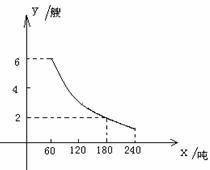
(1)这批货物的质量是多少吨?
(2)写出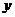 与
与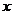 的函数关系式。
的函数关系式。
(3)如果要求出动货船不超过4艘,那么每艘货船的核定装载量至少要多少吨?
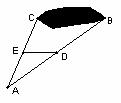
21.如下图,已知△ABC和△DEF是两个边长都为
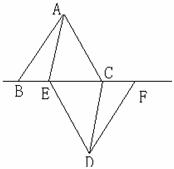
(1)求证:四边形AEDC是平行四边形。
(2)若△ABC沿着BF的方向匀速运动,△DEF不动,当△ABC运动到点B与点F重合时,四边形AEDC是什么特殊的四边形?说明理由。
五、学以致用(开动你的脑筋,只要你勇于探索,大胆实践,你一定会获得成功的!每题12分,共36分)
22.如下图,双曲线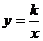 与直线
与直线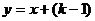 在第一象限的交点为A,在第三象限的交点为C,过A作AB⊥
在第一象限的交点为A,在第三象限的交点为C,过A作AB⊥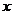 轴于点B,且
轴于点B,且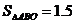 。
。
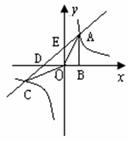
(1)求这两个函数的解析式;
(2)若点A的横坐标为1,点C的纵坐标为-1,求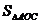 .
.
23.本市将进入汛期,部分路面积水比较严重。为了改善这一状况,市政公司计划将一段路的排水工程承包给甲、乙两工程队来施工。公司研究发现有不同施工方案:如果工程由甲、乙两队合作,则12天可以完成;若由某个工程队独做,则乙队单独完成这项工程所需时间是甲队单独完成这项工程所需时间的2倍。
(1)甲、乙单独完成这项工程所需时间分别需要多少天?
(2)若甲队每天需要工程费用650元,乙队每天需要工程费用400元,从节约资金的角度考虑,应选择哪种施工方案?
24.如图,在矩形ABCD中,AB=3,BC=4,点P在BC边上运动,连结DP,过点A作AE⊥DP,垂足为E。
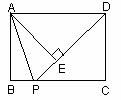
(1)连结AP,求证: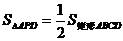
(2)设DP=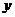 ,AE=
,AE=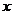 , 求
, 求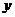 与
与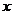 之间函数关系式;
之间函数关系式;
(3)写出自变量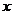 的取值范围,并求出
的取值范围,并求出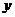 的最大值。
的最大值。