2009年雅安市初中毕业暨高中阶段教育学校招生考试
数学试卷
(本试卷满分120分,考试时间120分钟)
第Ⅰ卷(选择题 共36分)
一、选择题(本大题共l2小题,每小题3分,共36分.在每小题给出的四个选项中。只有一项是符合题目要求的)
1.如果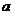 与3互为相反数,则
与3互为相反数,则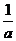 是 ( )
是 ( )
A.3 B.-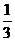 D.
D.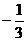
2.在下面的图形中,不是正方体的展开图的是 ( )

3.下列运算正确的是 ( )
A.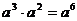 B.
B.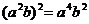
C.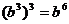 D.
D.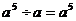
4.如图,AB∥CD,∠A=100°,∠D=25°,则∠AED= ( )
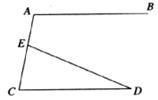
A.80° B.105° C.100° D.75°
5.已知单项式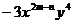 与
与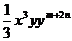 是同类项,则
是同类项,则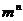 的值为
的值为
A.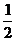 B.
B.
6.下列图形,既是中心对称图形又是轴对称图形的是 ( )
A.等边三角形 B.平行四边形 C.等腰梯形 D.矩形
7.在△ABC中,已知∠A,∠B都是锐角,且sinA=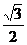 ,tanB=1,则∠C的度数为( )
,tanB=1,则∠C的度数为( )
A.75° B.105° C.60° D.45°
8.已知,在等腰梯形ABCD中,AD∥BC,AD=AB=2,∠B=60°,则梯形ABCD的周长为 ( )
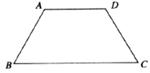
A.8 B.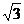 C.10 D.8+2
C.10 D.8+2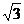
9.随意掷两枚均匀的相同骰子,面朝上的点数之和为10的概率是 ( )
A.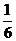 B.
B.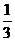 C.
C.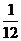 D.
D.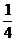
10.在平面直角坐标系中,若点P(3,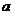 )和点Q(b,-4)关于
)和点Q(b,-4)关于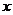 轴对称,则
轴对称,则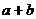 的值为 ( )
的值为 ( )
A.-7 B.7 C.1 D.-l
11.甲、乙两同学同时从学校出发,步行12千米到李村,甲比乙每小时多走l千米,结果甲比乙早到15分钟,若设乙每小时走x千米,则所列出的方程是 ( )
A.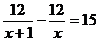 B.
B.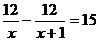
C.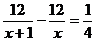 D.
D.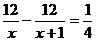
12.对于抛物线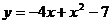 ,有下列说法:①抛物线的开口向上.②对称轴为
,有下列说法:①抛物线的开口向上.②对称轴为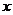 =2.③顶点坐标为(2,-3).④点(
=2.③顶点坐标为(2,-3).④点(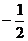 ,-9)在抛物线上.⑤抛物线与
,-9)在抛物线上.⑤抛物线与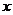 轴有两个交点.其中正确的有 ( )
轴有两个交点.其中正确的有 ( )
A.1个 B.2个 C.3个 D.4个
第Ⅱ卷(非选择题 共84分)
二、填空题(本大题共5小题,每小题3分,共15分.请把答案填在题中横线上)
13.计算:2 0082-2 009×2 007=________________.
14.已知: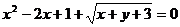 ,则
,则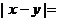 _______________.
_______________.
15.有4条线段长度分别为1 cm,2 cm,3 cm,4 cm,从中任取三条能构成三角形的概率为_______________.
16.如图,将△ABC沿BC方向平移得到△A’B’C’.已知BC=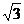 cm,△ABC与△A’B’C’,重叠部分(图中阴影部分)的面积是△ABC面积的
cm,△ABC与△A’B’C’,重叠部分(图中阴影部分)的面积是△ABC面积的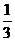 ,则△ABC平移的距离BB’是_______cm.
,则△ABC平移的距离BB’是_______cm.
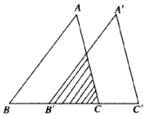
17.定义一种法则“*”如下: *
*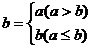 ,例如:1*2=2,若
,例如:1*2=2,若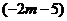 *3=3,则
*3=3,则 的取值范围是_________________
的取值范围是_________________
三、解答题(本大题共8小题,共69分.解答应写出文字说明、证明过程或演算步骤)
18.(本小题满分10分,每小题5分)
(1)计算: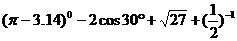
(2)先化简代数式: ,然后选取一个合适的
,然后选取一个合适的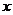 的值,代入求值.
的值,代入求值.
19.(本小题满分5分)
解不等式组,把它的解集在数轴上表示出来,并求该不等式组所有整数解的和.
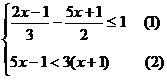
20.(本小题满分7分)
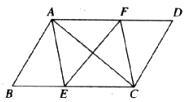
如图,平行四边形ABCD中,点E,F分别在BC,AD上,且∠BAE=∠DCF.
(1)求证:△ABE≌△,CDF.
(2)若AC⊥EF,试判断四边形AECF是什么特殊四边形?并证明你的结论.
21.(本小题满分8分)
我市某校为了了解八年级学生的身高情况,抽样调查了部分同学,将所得数据处理后,制成扇形统计图和频数分布直方图(部分)如下(每组只含最低值不含最高值,身高单位:cm,测量时精确到1 cm).
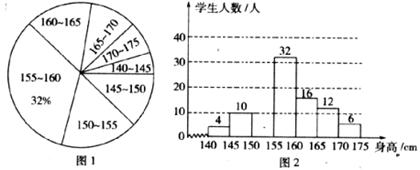
根据所提供的信息,解答下列问题:
(1)求本次抽样调查的学生人数:并补全频数分布直方图.
(2)该样本的中位数在统计图的哪个范围内?
(3)在统计图l中,求“身高在145―150 cm部分”的扇形所对应的圆心角的度数.
(4)如果该样本的平均数为l59 cm,方差为0.8;该校九年级学生身高的平均数为159 cm,方差为0.6,那么_______(填“八年级”或“九年级”)学生的身高比较整齐.
22.(本小题满分8分)
某学校计划购买若干台电脑,现从甲、乙两家商场了解到同一型号电脑每台报价均为4 000元,并且多买都有一定的优惠。甲商场的优惠条件是:第一台按原报价收费,其余每台优惠15%;乙商场的优惠条件是:每台优惠l0%.
(1)分别写出甲、乙两商场的收费y(元)与所买电脑台数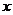 (台)之间的关系式.
(台)之间的关系式.
(2)该学校选择哪家商场购买更优惠?
23.(本小题满分9分)
如图,一次函数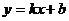 的图象与反比例函数
的图象与反比例函数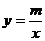 的图象相交于点C(2,2),与
的图象相交于点C(2,2),与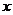 轴负半轴交于点A,与
轴负半轴交于点A,与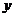 轴交于点B,O为坐标原点,且tan∠BAO=
轴交于点B,O为坐标原点,且tan∠BAO=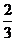 .
.
(1)求反比例函数与一次函数的表达式.
(2)求一次函数与反比例函数图象的另一交点D的坐标.

24.(本小题满分l0分)
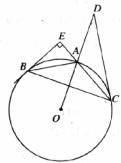
如图,△ABC内接于⊙O,过点B的切线与CA的延长线相交于点E,且∠BEC=90°,点D在OA的延长线上,AO⊥BC,∠ODC=30°.
(1)求证:DC为⊙O的切线.
(2)若CA=6,求DC的长.
25.(本小题满分12分)
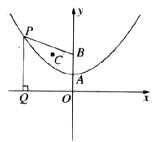
如图,抛物线的顶点A的坐标(0,2),对称轴为y轴,且经过点(-4,4).
(1)求该抛物线的表达式.
(2)若点B的坐标为(0,4),P为抛物线上一点(如图),过点P作.PQ⊥ 轴于点Q,连接PB,求证:PQ=PB.
轴于点Q,连接PB,求证:PQ=PB.
(3)若点C(-2,4),利用(2)的结论,判断抛物线上是否存在一点K,使△KBC的周长最小,若存在,求出这个最小值,并求此时点K的坐标;若不存在,请说明理由。