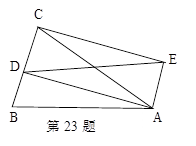
摘要:20. 如图.平行四边形ABCD中.点E.F分别在BC.AD上.且∠BAE=∠DCF. (1)求证:△ABE≌△,CDF. (2)若AC⊥EF.试判断四边形AECF是什么特殊四边形?并证明你的结论.
网址:http://m.1010jiajiao.com/timu_id_765044[举报]
(本小题满分10分)如图,已知抛物线经过A(-2,0),B(-3,3) 及原点![]() ,顶点为
,顶点为![]() .
.
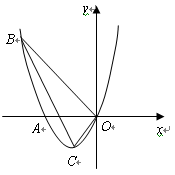
(1)求抛物线的解析式;
(2)若点![]() 在抛物线上,点
在抛物线上,点![]() 在抛物线的对称轴上,且以A、O、D、E为顶点的四边形是平行四边形,求点D的坐标;
在抛物线的对称轴上,且以A、O、D、E为顶点的四边形是平行四边形,求点D的坐标;
(3)![]() 是抛物线上第一象限内的动点,过点
是抛物线上第一象限内的动点,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,是否存在点
,是否存在点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,求出点
相似?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看习题详情和答案>>
(本小题满分8分)如图,四边形ABCD是平行四边形,AC、BD交于点O,∠1 =∠2.
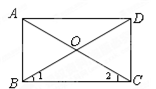
(1)求证:四边形ABCD是矩形;
(2)若∠BOC=120°,AB = 4cm,求四边形ABCD的面积.
查看习题详情和答案>>
(本小题满分8分)
如图,抛物线(
>0)与y轴交于点C,与x轴交于A 、B两点,点 A在点B的左侧,且
.

(1)求此抛物线的解析式;
(2)如果点D是线段AC下方抛物线上的动点,设D点的横坐标为x,
△ACD的面积为S,求S与x的关系式,并求当S最大时点D的坐标;
(3)若点E在x轴上,点P在抛物线上,是否存在以A、C、E、P为顶点的平行四边形?若存在求点P坐标;若不存在,请说明理由.
查看习题详情和答案>>