2008-2009学年度日照实验学校第二学期初二期末终结性评价
数学试卷
一、相信你的选择
1．若分式
的值为0，则x的值为（ ）
A．1 B．
2．若点（x0，y0）在函数y=
（ x＜0）的图象上，且x0y0=－2，则它的图象大致是 （ ）
A． B． C． D．
3．某鞋店试销一款女鞋，试销期间对不同颜色鞋的销售情况统计如下表：
颜色
黑色
棕色
白色
红色
销售量（双）
60
50
10
15
鞋店经理最关心的是哪种颜色的鞋最畅销，则对鞋店经理最有意义的统计量是 （ ）
A．平均数 B．众数 C．中位数 D．方差
4．给出下面四个命题：（1）一组对边平行的四边形是梯形；（2）一条对角线平分一个内角的平行四边形是菱形；（3）两条对角线互相垂直的矩形是正方形；（4）一组对边平行另一组对边相等的四边形是平行四边形（5）一组对边相等，一组对角相等的四边形是平行四边形．其中真命题的个数有（ ）
A．2个 B．3个 C．4个 D．5个
5．如图，已知四边形ABCD是平行四边形，下列结论中不正确的是（ ）
A．当AB=BC时，它是菱形
B．当AC⊥BD时，它是菱形
C．当∠ABC=900时，它是矩形
D．当AC=BD时，它是正方形
6．函数
与函数
在同一坐标系中的大致图象是（ ）
A． B． C． D．
7．菱形的两条对角线的长分别是6和8 ，则这个菱形的周长是（ ）
A．24 B．20 C．10 D．5
8．如图，在Rt△ABC 中，
，D、E是斜边BC上两点，且∠DAE=45°，将△
绕点
顺时针旋转90
后，得到△
，连接
，下列结论：
①△
≌△
； ②△
≌△
；
③
； ④
其中正确的是（ ）
A．②④； B．①④； C．②③； D．①③．
9．如图，A、B是函数
的图象上关于原点O对称的任意两点，AC平行于y轴，交x轴于点C，BD平行于y轴，交x轴于点D，设四边形ADBC面积为S，则（ ）
A．
B．1＜S＜2 C．S=2 D．S＞2
10．两位同学在描述同一反比例函数的图象时，甲同学说：这个反比例函数的图象上任意一点到两坐标轴的距离的积都是3；乙同学说：这个反比例函数的图象与直线y=x有两个交点，你认为这两位同学所描述的反比例函数的解析式是（ ）
A．
B．
C．
D．
11．数据
，
，
，，
，，的中位数是（ ）
A． B．
C． D．
12．如图，有一块直角三角形纸片，两直角边AC=6，BC=8，现将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，则CD等于（ ）
A．2cm B．3cm C．4cm D．5cm
二、试试你的身手
13．写出一个含有字母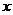
的分式（要求：不论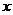取任何实数，该分式都有意义）
．
14．在下列三个不为零的式子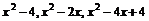 
中，任选两个你喜欢的式子组成一个分式是
，把这个分式化简所得的结果是
.
15．如图（1）是一个等腰梯形，由6个这样的等腰梯形恰好可以拼出如图（2）所示的一个菱形．对于图（1）中的等腰梯形，请写出它的内角的度数或腰与底边长度之间关系的一个正确结论： ．
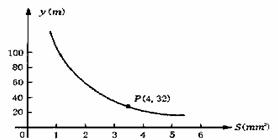
16．你吃过拉面吗？实际上在做拉面的过程中就渗透着数学知识：一定体积的面团做成拉面，面条的总长度y（m）是面条的粗细（横截面积）S（mm2）的反比例函数，其图象如图所示．则当面条粗1.6mm2时，面条的总长度是 。
17．点A（m，m＋1），B（m＋3，m－1）都在反比例函数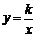
的图象上．则
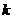＝ 。18．用你发现的规律解答下列问题．
┅┅
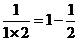
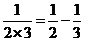
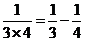
（1）探究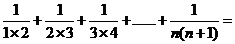
．（用含有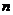
的式子表示）
（2）若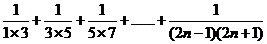
的值为
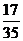，则= ．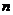
三、挑战你的技能
19．（1）先化简，再求值：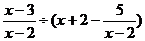
，其中x＝－4．
（2）若关于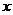的分式方程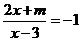
无解，求m的值。
20．甲、乙两同学玩“托球赛跑”游戏，商定：用球拍托着乒乓球从起跑线
起跑，绕过P点跑回到起跑线（如图所示）；途中乒乓球掉下时须捡起并回到掉球处继续赛跑，用时少者胜．结果：甲同学由于心急，掉了球，浪费了6秒钟，乙同学则顺利跑完．事后，甲同学说：“我俩所用的全部时间的和为50秒”，乙同学说：“捡球过程不算在内时，甲的速度是我的1.2倍”．根据图文信息，请问哪位同学获胜？
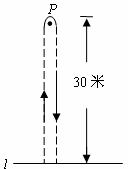
21．为预防“手足口病”，某校对教室进行“药熏消毒”．已知药物燃烧阶段，室内每立方米空气中的含药量
（mg）与燃烧时间（分钟）成正比例；燃烧后，与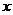成反比例（如图所示）．现测得药物10分钟燃完，此时教室内每立方米空气含药量为8mg．据以上信息解答下列问题：
（1）求药物燃烧时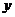与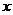的函数关系式．
（2）求药物燃烧后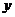与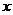的函数关系式．
（3）当每立方米空气中含药量低于1.6mg时，对人体方能无毒害作用，那么从消毒开始，经多长时间学生才可以回教室？
23．如图甲，在△ABC中，∠ACB为锐角．点D为射线BC上一动点，连接AD，以AD为一边且在AD的右侧作正方形ADEF．
（1）如果AB=AC，∠BAC=90º．解答下列问题：
①当点D在线段BC上时（与点B不重合），如图乙，线段CF、BD之间的位置关系为 ，数量关系为 ．
②当点D在线段BC的延长线上时，如图丙，①中的结论是否仍然成立，请说明理由。
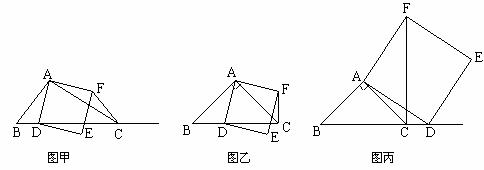
（2）如果AB≠AC，∠BAC≠90º，点D在线段BC上运动．
试探究：当△ABC满足一个什么条件时，CF⊥BC（点C、F重合除外）？不用说明理由．
∴
≥
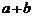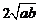，只有当a＝b时，等号成立．
结论：在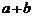≥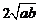（a、b均为正实数）中，若ab为定值p，则a+b≥
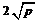，只有当a＝b时，a+b有最小值．
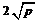（1）根据上述内容，回答下列问题：
若m＞0，只有当m＝ 时，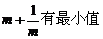
．
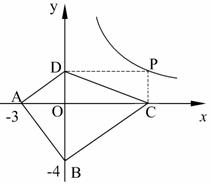
（2）探索应用：如图，已知A（－3，0），B（0，－4），P为双曲线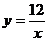
（x＞0）上的任意一点，过点P作PC⊥x轴于点C，PD⊥y轴于点D．求四边形ABCD面积的最小值，并说明此时四边形ABCD的形状．
