2009年聊城市莘县初三春季诊断性检测(一)
数学试卷
说明:本试题满分120分,考试时间120分钟。
一、选择题(每题3分,共36分)
1.下列计算正确的是
A.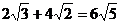 B.
B.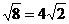
C.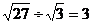 D.
D.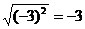
2.2008奥运会国家体育馆“鸟巢”的建筑面积达25.8万m2,用科学记数法表示应是
A.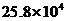 m2 B.
m2 B.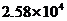 m
m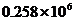 m2 D.
m2 D.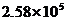 m2
m2
3.一个正方体的每个面都写有一个汉字,其展开图如下图所示,则在该正方体中和“迎”相对面上所写的汉字是
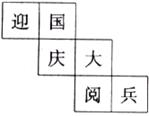
A.大 B.阅 C.兵 D.庆
4.如下图,以O为圆心的两个同心圆中,大圆的弦AB切小圆于点P,且AB=4,则圆环的面积(阴影)是
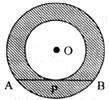
A.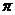 B.
B.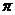 C.3
C.3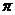 D.4
D.4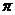
5.如下图,将圆沿AB折叠后,圆弧恰好经过圆心,则 的度数等于
的度数等于
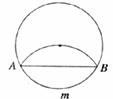
A.60° B.90° C.120° D.150°
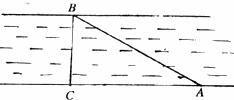
6.已知如下图,小明为测村附近小河的宽度,在河岸上取了两点A、C,并使AC⊥BC,若测得AC=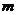 ,
,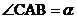 ,则河宽BC=
,则河宽BC=
A.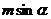 B.
B.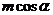 C.
C.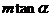 D.
D.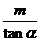
7.为贯彻两会的教育改革精神,某县加强了教育经费投入,2007年投入3000万元,预计2009年投入5000万元,设每年教育经费的平均增长率为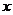 ,则列方程为
,则列方程为
A.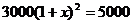 B.
B.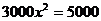
C.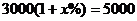 D.
D.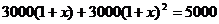
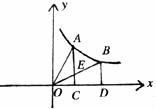
8.如下图,过反比例函数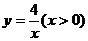 图像上两点A、B,分别作
图像上两点A、B,分别作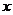 轴的垂线,垂足分别为C、D两点,连OA、OB,设AC与OB交于点E,△AOE与梯形ECDB的面积分别为
轴的垂线,垂足分别为C、D两点,连OA、OB,设AC与OB交于点E,△AOE与梯形ECDB的面积分别为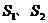 ,则
,则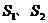 大小关系是
大小关系是
A.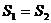 B.
B.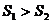
C.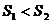 D.
D.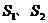 大小不确定
大小不确定
9.已知:如下图,抛物线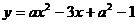 ,那么
,那么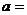
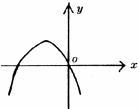
A.1 B.-1 C.±1 D.0
10.如下图,一扇形花纸片OAB,已知OA=60cm,∠AOB=120°,小明将OA、OB合拢成一个圆锥形的生日帽(接缝忽略不计),则生日帽的底面半径为
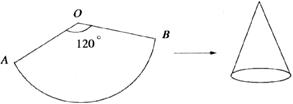
A.10cm B.20cm C.24cm D.30cm
11.小华的哥哥在西藏工作,今年“五一”她想让哥哥带几本科技书回家,于是发短信告之,可一时记不清哥哥手机号码后三位数字的顺序,只记得是0、2、8三个数字,则小华一次发短信成功的概率是
A.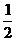 B.
B.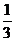 C.
C.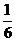 D.
D.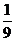
12.在密码学中,能看到的为明码,对明码处理后得到的内容为密码,有一密码,将26个英文字母a、b、c……z(不论大小写)依次对应1、2……26(见表格),当明码号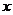 为奇数时,密码号
为奇数时,密码号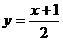 ,当明码号
,当明码号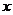 为偶数时,密码号
为偶数时,密码号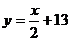
字母
a
b
c
d
e
f
g
h
i
j
k
l
m
n
o
p
q
r
s
t
u
v
w
x
y
z
序号
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
按上述规定,将明码love译成密码是
A.gawq B.shxc C.sdri D.love
二、填空(3×5=15分,只要求写出最后结果)
13.两圆的半径分别为3、4,圆心距为1,则两圆的位置关系是__________。
14.对于实数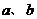 ,定义一种新运算
,定义一种新运算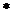 为:
为: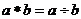 ,则
,则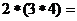 __________。
__________。
15.飞机着陆后滑行距离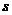 (米)与滑行时间
(米)与滑行时间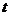 (秒)满足:
(秒)满足: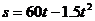 ,那么飞机着陆后滑行__________秒,才能停下来。
,那么飞机着陆后滑行__________秒,才能停下来。
16.若关于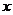 的分式方程
的分式方程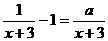 有增根,则
有增根,则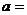 __________。
__________。
17.已知关于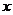 的不等式组
的不等式组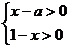 的整数解只有2个,则
的整数解只有2个,则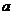 的取值范围是__________。
的取值范围是__________。
三、解答题(共69分,步骤要合理)
18.(6分)先化简,再选一个你喜欢的值代入(要适合哟!)
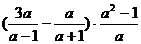
19.(8分)如下图,E为正方形ABCD的边AB上的动点,EF⊥DE交BC于点F。
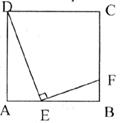
(1)求证:△ADE∽△BEF
(2)设正方形的边长为4,AE=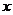 ,BF=
,BF=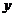 ,当
,当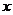 为何值时,
为何值时,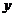 有最大值?最大值是多少?
有最大值?最大值是多少?
20.(8分)如下图,点A、B、D、E在⊙O上,弦AE、BD的延长线交于点C,若AB是⊙O的直径,D为BC中点。
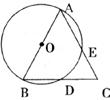
(1)试判断AB、AC大小,并证明。
(2)在上述题设条件下,△ABC还须满足什么条件,点E一定是AC的中点?(直接写出结论)
21.(8分)2008北京奥运会刚刚过去,2012年伦敦奥运会已在向世人招手。某校学生会,为了了解全校同学最想收看伦敦奥运会哪种比赛项目的情况,随机调查了200名同学,根据调查结果作了频数分布表:
最想收看的项目
频率(人数)
频率
足球
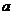
0.14
篮球
36
0.18
排球
16
0.08
羽毛球
30
0.15
乒乓球
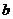
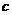
游泳
16
0.08
跳水
20
0.10
田径
2
0.01
合计
200
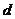
(1)补全频数分布表。
(2)根据统计结果,请写出至少两条正确的结论。
(3)据以上信息,作为中学生的你,对中国体育的发展有何建议?
(4)根据以上调查估计,该校5100名学生中,最想收看游泳比赛的人数是多少?
22.(8分)在一次数学课上,老师让同学们把矩形ABCD折叠,使B、D两点重合,折痕为直线MN,折痕与AD、BC分别交于M、N两点。
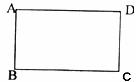
试问:(1)你能在图上用尺规作图画出其折痕吗?(保留作图痕迹即可)
(2)若AB=1cm,AD=2cm,AM的长是多少呢。
23.(10分)甲、乙两人骑自行车同时前往A地,他们距A地的距离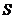 (km)与行驶时间
(km)与行驶时间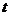 (h)之间的关系如图。
(h)之间的关系如图。
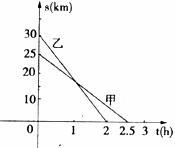
(1)甲、乙两人的速度各是多少?
(2)写出甲、乙两人距A地的距离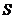 与行驶时间
与行驶时间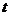 的关系式(任选一个)
的关系式(任选一个)
(3)出发多长时间甲与乙相遇?
24.(10分)如下图,某幼儿园为了加强安全管理,决定将园内滑滑板的倾斜角由45°降为30°,已知原滑滑板AB长5米,点D、B、C在同一水平地面上。
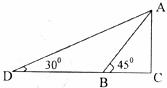
(1)改善后的滑滑板会加长多少?(保留3个有效数字)
(2)若滑滑板的正前方能有3米的空地就能保证安全,原滑滑板的前方有6米长的空地,像这样改造是否可行?说明理由。(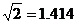 、
、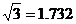 、
、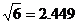 )
)
25.(11分)如下图,在平面直角坐标系中,等腰梯形AOBC的四个顶点坐标分别为A(2,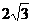 )、O(0,0)、B(8,0)、C(6,
)、O(0,0)、B(8,0)、C(6,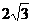 )。
)。
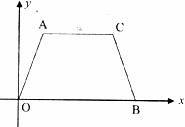
(1)求等腰梯形AOBC的面积。
(2)试说明点A在以OB为直径的圆上。
(3)在第一象限内确定一点M,使△MOB与△AOB相似,求出所有符合条件的点M 的坐标。